|
| -204 | 0 | 204 | 294 | 408 | 498 | 702 | 792 | 906 | 996 | 1200 | ||||||||||||||||||||
| *NI1 | SA | RI4 | GA4 | |||||||||||||||||||||||||||
| GA1 | MA1 | PA | DHA4 | |||||||||||||||||||||||||||
| DHA1 | NI1 | SA* | ||||||||||||||||||||||||||||
Éléments d'harmonie
Cet article visait à introduire à l'étude de l'harmonie, à la
conception des instruments de musique, à l'éducation de l'oreille et
à la compréhension de principes sur lesquels le solfège repose. Il
m'a servi à préparer ce que j'ai publié au printemps 2006 sur le forum de
Radio Teentaal. L'annexe provient de ce deuxième travail.
SAVANTS
ET MUSICIENS QUI ONT FAIT PROGRESSER LA THÉORIE DE LA MUSIQUE
- Pythagore (v. 580-504 av. J.-C.), grec né dans l’île de Samos.
- Aristoxène (IVème siècle av. J.-C.), grec
de Tarente en Italie.
Son père et son grand-père étaient disciples de Pythagore. Aristoxène
écrivit 300 livres. Dans son entourage vivait un certain Archytias.
Aristoxène affectionnait les instruments à corde.
S'il n'aimait pas les instruments à vents, c'est parce que le fonctionnement de ceux-ci était trop
difficile à comprendre.
- Gui d’Arezzo (995-1050), moine italien, inventa la
portée
La portée, c'est le support de l’écriture de la musique.
- Giossefe Zarlino (1517-1590), écrivit les Institutions harmoniques (1558).
- John Neper (1517-1550), baron écossais, inventa les
logarithmes puis son fils en étudia les propriétés.
Tout se passe comme si le logarithme était une fonction mathématique qui
transforme une multiplication en addition, et une division en soustraction.
- Nikolaus Kauffmann (1620-1687), astronome et
physicien allemand, a découvert la série logarithmique.
Kauffmann (en allemand) = Marchand (en français) = Mercator (en latin).
- Nicholas Mercator (ca1640-1694) [fils du précédent ?] a fait faire des progrès vers le tempérament égal.
(Cf. Genesis of a music,
de Harry Partch, éd. 1947 augmentée, p. 383).
Le Mercator cartographe est Gerhard Kremer, mathématicien et
géographe flamand, 1512-1594 ; ce n'est pas la même personne.
- Le frère Mersenne (+1688) est l'auteur du traité De l'harmonie universelle.
- Werckmeister (1644-1706) a inventé la gamme tempérée en 1691.
- William Holder (1616–1698), en 1694, a partagé le "ton pythagoricien"
en 9 commas, le demi-ton diatonique en valant 4 et le demi-ton chromatique en valant 5.
- Jean-Sébastien Bach (1685-1750), musicien et organiste allemand, a mis cela en pratique.
- Leonhardt Euler (1707-1783), mathématicien suisse, a proposé d’utiliser les logarithmes pour décrire et étudier plus facilement les rapports de hauteur entre les sons.
- Félix Savart (1791-1841), médecin et physicien français, a mesuré le pouvoir discriminant de l’oreille humaine quant aux hauteurs de son.
- Heinrich Rudolf Hertz (1857-1894) est un physicien
allemand.
On a donné son nom à l’unité légale de fréquence (le Hertz ;
symbole Hz ; 1 Hz = 1 aller-retour par seconde).
- Hermann von Helmholtz
(1821-1894), a écrit en allemand une thèse intitulée les Tonenpfindungen.
Traduite en anglais, celle-ci a été publiée à Londres en 1885 sous le
titre On the Sensations of Tone as a
Physiological Basis for the Theory of Music.
- James Murray Barbour est le
chercheur américain qui a écrit une thèse intitulée Equal temperament :
its history from Ramsis (1482) to Rameau (1737).
Le manuscrit de celle-ci, daté de 1932, se trouve à la bibliothèque de l’Université
de Cornell, Ithaca, U.S.A. .
Un peu de maths, un peu d'histoire...
Rappel de mathématiques : notion de fonction
Rappelons qu'une fonction, c'est par définition toute
correspondance particulière entre des éléments d'un ensemble de départ --
ces éléments peuvent être des nombres -- et des éléments d'un ensemble
d'arrivée -- ces éléments peuvent aussi être des nombres --, de façon à ce
que tout élément de l'ensemble de départ ait un correspondant et un
seul dans l'ensemble d'arrivée (un élément de l'ensemble de départ a
un correspondant et un seul dans l'ensemble d'arrivée, par contre, chaque
élément de l'ensemble d'arrivée peut avoir un ou plusieurs correspondants
dans l'ensemble de départ).
Rappel de mathématiques : fonction inverse
La fonction inverse, par définition, c'est la fonction y(x)
définie par la formule : y = 1/x .
Rappel de mathématiques : fonction Logarithme
La fonction Logarithme, par définition, c'est la primitive de
cette fonction inverse.
Pour ne pas alourdir inutilement les rappels de mathématiques, on n'exposera
pas ici, ce qu'est la dérivée d'un fonction. On dira seulement que la
primitive, c'est la notion inverse de la notion de dérivée et on invitera tous
ceux qui souhaitent rafraîchir leurs connaissances en maths à lire vite fait :
http://www.cyberprofs.fr/logarithme_exponentielle.htm
.
Note historique
C'est Neper, un Écossais, qui, au XVII° siècle a trouvé - ou redécouvert - la fonction Log.
L'application des logarithmes à la musique a été proposée
au XVIII° siècle par le mathématicien
Euler (1707-1783), un Allemand, après que Werckmeister (1645-1706) eût proposé de réduire
un tout petit peu les quintes, de façon à ce que 12 quintes faibles puissent
égaler exactement 7 octaves. C'est Euler, le premier, qui a proposé
d'appliquer aux rapports de fréquences entre les vibrations sonores la
propriété remarquable des logarithmes énoncée plus haut.
Au milieu du XVIII°, les "élémens de musique théorique et pratique", un manuel
approuvé par Condillac en novembre 1751 et publié à Paris en 1752, et dont on
sait qu'il a été écrit par Jean Le Rond d'Alembert, manuel qui vulgarise les théories de
Jean-Philippe Rameau, présente les échelles non tempérées et l'échelle
tempérée. Ce manuel est l'un des ouvrages de référence de l'exposé qui va
suivre. On y trouve décrite une description d'accorder le clavecin à la mode
de Werckmeister (sans que celui-ci soit nommé) et la justification théorique
avec les nombres racine de deux, racine cubique de deux, racine quatrième
de deux, etc. jusqu'à racine douzième de deux.
L'échelle tempérée va permettre de faire avancer d'un grand pas la conception des orgues : ceci vont pouvoir devenir plus grands et plus complexes. Pourquoi la convention d'avoir pris un LA comme note de référence ? On dit que c'est parce ce LA est en plein milieu de l'ensemble des notes jouées par l'orgue.
L'échelle tempérée va aussi permettre l'éclosion de la musique d'orchestre au XIX° siècle.
De nos jours, les échelles non tempérées ne sont plus enseignées.
On trouve encore dans la littérature des traces de débats qui remontent à la plus haute Antiquité mais qui sont brouillons et passionnés et où, par ignorance, beaucoup de ceux qui y prennent part mélangent tout. On en trouve trace aussi dans le solfège.
Fournir des éléments pour y voir clair est le but du présent exposé.
Les principales applications pratiques sont la compréhension de la conception des instruments de musique et la composition musicale.
Pour celle-ci, le lecteur pourra utiliser les logiciels
- Pizzicato
(de chez Arpège-Musique à Liége ; disponible gratuitement sur l'internet,
mais à l'essai seulement : http://www.arpegemusique.com/
)
- et Zarlino
(du Suisse Olivier Bettens et de deux
Français, téléchargeable gratuitement depuis l'internet à l'adresse suivante
: http://virga.org/zarlino/
).
Ce petit exposé tout modeste est du genre des écrits de théorie de la musique de mes illustres prédécesseurs : dans l'Antiquité Pythagore - qu'on ne connaît que par Boèce -, Aristoxène de Tarente et Ptolémée, puis Zarlino au XVI° - controverse avec Galilée -, le père Mersenne au XVII°, Rameau et d'Alembert au XVIII°, au XIX° Helmholtz et au XX° Olivier Bettens.
Il utilise évidemment la mesure du pouvoir discriminant de
l'oreille effectuée par Savart et la proposition faite par Ellis au XIX° de représenter l'octave par une échelle
de 1200 "cents" ;
nous dirons ici 1200 points ; avec un barreau
tous les 100 points.
Allez, encore un peu de maths !...
Rappelons une propriété caractéristique et essentielle de la
fonction logarithme : celle-ci permet de transformer une multiplication en
addition et une division en soustraction.
En effet :
Log (a b) = Log a + Log b
Log (a / b) = Log a - Log b
Soit la fonction y = (1200 / Log 2) Log x
Application numérique :
x = 2 ==> y = 1200 ; x
= 3 ==> y = 1902 ; x = 5 ==> y = 2786
x = 3/2 ==> y = 702 ; x =
5/4 ==> y = 386 ; x = 1/2 ==> y = - 1200
etc. (on trouvera plein de détails dans la
suite).
De la propriété fondamentale de la fonction
logarithme, on tire que :
Log an = n Log a
Par exemple : Log a 12 = 12 Log a ; et aussi : Log a-12 = -12 Log a
a 12, c'est a multiplié 12
fois par lui-même ; a-12 = 1 / a 12
(autrement dit : a- 12 est l'inverse de a12)
;
a1/12, c'est le nombre qui, multiplié 12 fois par lui
même, est tel que le résultat de cette multiplication est a.
Ainsi, par exemple,
a2, c'est le carré de a
a1/3, c'est la racine cubique de a
On dit aussi (et on note)
"racine n-ième de a
" pour "a puissance 1/n" ; c'est la même chose :
"racine n-ième de
a" = "a puissance 1/n"
Par contre :
"a puissance -n", c'est
"1 / a puissance n" (et en effet, Log 1 = 0)
Les nombres
x = racine 12ème de 20 qui est 1, c'est 1
x = racine 12ème de 21, c'est-à-dire racine 12ème de 2
x = racine 12ème de 22,
x = racine 12ème de 23,
etc.
ont pour image par la fonction définie plus haut
[ y = (1200 / Log 2). Log x ] :
y = 0
y = 100,
y = 200,
y = 300,
etc.
Au passage remarquons que
"racine n-ième de
(a puissance p)" = "(racine n-ième de a )puissance p)"
(en effet :
chacun des deux membres de cette égalité peut aussi s'écrire
"a p/n" )
Juste un peu de physique, d'acoustique et de physiologie, et... encore des maths !
Toute fréquence f, notre oreille :
a) la reconnaît plus ou moins selon sa hauteur absolue - ça dépend des gens
b) reconnaît son écart relatif à une fréquence qu'on vient de lui donner
comme référence ou qu'elle a pris comme référence - c'est vrai pour tout le
monde.
Dans ce qui suit, on s'intéresse le plus souvent au rapport entre une fréquence f donnée et toute fréquence fo prise comme référence : x = (f / fo). On est le plus souvent dans le domaine du relatif.
Convenir que fréquence fo vaut 1,
c'est convenir que Log fo =
0
(puisque Log 1 = 0)
et c'est faire de fo un zéro de l'échelle
dans un monde image du monde réel (le monde de la représentation du réel). Il
suffit de donner à fo sa vraie valeur en hertz pour avoir alors la valeur
en hertz de toutes les autres fréquences qu'on aura considérées.
La racine douzième de deux, elle est égale à
1,059 463
094 358.
Soit a cette valeur.
(Dans les calculs qui suivent, on la confondra avec sa valeur arrondie par
défaut, à neuf chiffres après la virgule seulement, au lieu de douze).
Celle ci élevée au carré [= a2], c'est la racine sixième de deux.
Il est facile de calculer le tableau suivant :
Pour en faciliter la lecture, on ajoute une colonne où l'on met une valeur
approchée de x.
Attention cependant, dans des calculs que l'on pourrait être amener à
effectuer par la suite, cet arrondi à deux chiffres ne sera pas satisfaisant.
|
x |
y |
x arrondi |
|
| a0 | 1, 000 000 000 | 0 | 1,00 |
| a1 | 1, 059 463 094 | 100 | 1,06 |
| a2 | 1, 122 462 048 | 200 | 1,12 |
| a3 | 1, 189 207 115 | 300 | 1,19 |
| a4 | 1, 259 921 050 | 400 | 1,26 |
| a5 | 1, 334 839 854 | 500 | 1,33 |
| a6 | 1, 414 213 562 | 600 | 1,41 |
| a7 | 1, 498 307 077 | 700 | 1,50 |
| a8 | 1, 587 401 052 | 800 | 1,59 |
| a9 | 1, 681 792 830 | 900 | 1,68 |
| a10 | 1, 781 797 436 | 1000 | 1,78 |
| a11 | 1, 887 748 625 | 1100 | 1,89 |
| a12 | 2, 000 000 000 | 1200 | 2,00 |
Fonction réciproque
Étant donnée une valeur de
y,
comment trouver la valeur de x ?
La fonction réciproque de la fonction Logarithme,
c'est la fonction
Exponentielle.
Autrement dit : Exponentielle {Logarithme (z)] = z ; ce qu'on note : e Log z = z
Reprenons la définition de la fonction y :
y = (1200 / Log 2) Log x
On a donc : y / (1200 / Log 2) = Log x ;
c'est-à-dire y ( Log
2 / 1200 ) = Log x
égalité qui s'écrit aussi : Log x = (Log 2 / 1200 ) y
et d'où on tire, puisque e Log x = x :
x = e ( Log 2 / 1200) y
Ainsi, nous avons désormais moyen de passer de x à y, (quelle que soit la valeur de fo prise étant égale à l'unité), puis de repasser d'un valeur de y à une valeur de x. Et dans tous les cas de trouver la valeur de f, une fois choisie celle de fo puisqu'on a posé x = f /fo .
APPLICATION A LA MUSIQUE
In Élémens
de musique théorique et pratique, Paris, 1752, op. cit.**, au chapitre consacré à l'accord du clavecin,
après avoir parlé de la très légère diminution des quintes*, d'Alembert, poursuit
:
Tous les
demi-tons étant égaux dans le tempérament que M. Rameau propose, il s'ensuit
que les douze demi-tons ut, ut#, ré, ré#, mi, mi#, etc. formeront une suite géométrique
continue, c'est-à-dire une suite dans laquelle ut sera à ut# dans le même
rapport que ut# à ré, que ré à ré#, etc., & ainsi de suite.
Ces douze demi-tons sont formés par une suite de treize sons dont un ut grave
et son octave ut aigu sont le premier et le dernier.
Ainsi, pour trouver par le calcul la valeur de chaque son dans le tempérament
dont il s'agit, la question se réduit à trouver entre les nombres 1 et 2 onze
autres nombres qui fassent avec 1 et 2 une progression géométrique continue.
Pour peu qu'on ait l'usage du calcul, on trouvera facilement chacun de ces
nombres.
En voici l'expression, que les Mathématiciens reconnaîtront facilement, et que
les autres peuvent passer.
[* : celle-là même que
Werckmeister avait proposé]
[** : page 45, note u]
|
ut |
ut# |
ré |
ré# |
mi |
fa |
fa# |
sol |
sol# |
la |
la# |
si |
ut |
|
racine douzième de 20 |
racine douzième de 21 |
racine douzième de 22
|
racine douzième de 23 |
racine douzième de 24 |
racine douzième de 25 |
racine douzième de 26 |
racine douzième de 27 |
racine douzième de 28 |
racine douzième de 29 |
racine douzième de 210 |
racine douzième de 211 |
racine douzième de 212 |
|
= 1 |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= |
= 2
|
D'où il vient, puisque a =
racine douzième de 2
(la 4ème colonne se déduit du fait de l'égalité des demi-tons).
|
x |
y |
|
|
|
|
a0 |
1, 000 000 000 |
0 |
do |
|
|
a1 |
1, 059 463 094 |
100 |
do# |
réb |
|
a2 |
1, 122 462 048 |
200 |
ré |
|
|
a3 |
1, 189 207 115 |
300 |
ré# |
mib |
|
a4 |
1, 259 921 050 |
400 |
mi |
|
|
a5 |
1, 334 839 854 |
500 |
fa |
|
|
a6 |
1, 414 213 562 |
600 |
fa# |
solb |
|
a7 |
1, 498 307 077 |
700 |
sol |
|
|
a8 |
1, 587 401 052 |
800 |
sol# |
lab |
|
a9 |
1, 681 792 830 |
900 |
la |
|
|
a10 |
1, 781 797 436 |
1000 |
la# |
sib |
|
a11 |
1, 887 748 625 |
1100 |
si |
|
|
a12 |
2, 000 000 000 |
1200 |
do |
|
Voici comment calculer les fréquences de l'échelle tempérée
sur ordinateur personnel à l'aide d'un tableur (Excel, par exemple).
La
méthode qui est employée est celle qui consiste à calculer le do grave à
partir du la, puis à calculer toutes les autres fréquences à partir de ce do.
| A1 | B | C | D | E | F | G | H | I | J |
| 2 | |||||||||
| 3 | x relatif | y |
diapason (Hz) |
Hz | formule de la colonne I | ||||
| 4 | a0 | 1,000000000 | 0 | do | 261,625565379536 | '=H13/D13 | |||
| 5 | a1 | 1,059463094 | 100 | do# | réb | 277,182630966503 | '=H5*$I$4 | ||
| 6 | a2 | 1,122462048 | 200 | ré | 293,664767925072 | '=H6*$I$4 | |||
| 7 | a3 | 1,189207115 | 300 | ré# | mib | 311,126983815242 | '=H7*$I$4 | ||
| 8 | a4 | 1,259921050 | 400 | mi | 329,627557039829 | '=H8*$I$4 | |||
| 9 | a5 | 1,334839854 | 500 | fa | 349,228231493887 | '=H9*$I$4 | |||
| 10 | a6 | 1,414213562 | 600 | fa# | solb | 369,994422725658 | '=H10*$I$4 | ||
| 11 | a7 | 1,498307077 | 700 | sol | 391,995436132285 | '=H11*$I$4 | |||
| 12 | a8 | 1,587401052 | 800 | sol# | lab | 415,304697713570 | '=H12*$I$4 | ||
| 13 | a9 | 1,681792830 | 900 | la |
440 |
440,000000000000 | '=H13*$I$4 | ||
| 14 | a10 | 1,781797436 | 1000 | la# | sib | 466,163761585308 | '=H14*$I$4 | ||
| 15 | a11 | 1,887748625 | 1100 | si | 493,883301310067 | '=H15*$I$4 | |||
| 16 | a12 | 2,000000000 | 1200 | do | 523,251130759072 | '=H16*$I$4 | |||
| 17 | |||||||||
Avec Excel, il n'y en a alors plus que pour un instant à
calculer les fréquences pour différentes valeurs de diapason, par exemple 440,
435 et 415 Hz.
Les voici :
| y | série 440 | série 435 | série 415 | ||
| 0 | do | 261,6255654 | 258,6525476 | 246,7604764 | |
| 100 | do# | réb | 277,1826310 | 274,0328283 | 261,4336178 |
| 200 | ré | 293,6647679 | 290,3276683 | 276,9792697 | |
| 300 | ré# | mib | 311,1269838 | 307,5914499 | 293,4493143 |
| 400 | mi | 329,6275570 | 325,8817893 | 310,8987186 | |
| 500 | fa | 349,2282315 | 345,2597289 | 329,3857183 | |
| 600 | fa# | solb | 369,9944227 | 365,7899406 | 348,9720123 |
| 700 | sol | 391,9954361 | 387,5409425 | 369,7229682 | |
| 800 | sol# | lab | 415,3046977 | 410,5853261 | 391,7078399 |
| 900 | la | 440,0000000 | 435,0000000 | 415,0000000 | |
| 1000 | la# | sib | 466,1637616 | 460,8664461 | 439,6771842 |
| 1100 | si | 493,8833013 | 488,2709911 | 465,8217501 | |
| 1200 | do | 523,2511308 | 517,3050952 |
493,5209529 |
|
La conversion en points donnée par la fonction y = (1200 / Log
2) Log x
[ qu'on peut aussi retenir - c'est peut-être plus facile - sous sa forme y =
1200 (Log x /Log 2) ]
va nous permettre de comparer facilement entre elles les valeurs de ce tableau.
Souvenons-nous en effet, que x, nous l'avons toujours posé comme étant un
rapport de fréquences.
Proposons nous de comparer chaque valeur de la colonne de la série 435 à chaque valeur homologue de la série 440 (autrement dit, nous voulons comparer le do relatif au la 440 au do relatif au la 435, le sol relatif au la 440 au sol relatif au la 435, et de même pour toutes les valeurs du tableau). De plus, nous voulons comparer aussi le do relatif au la 415, au do relatif au la 440, et de même pour toutes les lignes du tableau.
Considérer la structure de nos tableaux, se souvenir de la
façon dont nous les avons conçus, va nous dispenser de calculs et nous
conduire rapidement au résultat. En effet :
- nous avons posé : a = racine douzième de 2 ;
- nous avons construit DO = LA / a9 ;
- puis nous avons calculé :
--- DO# = a. DO = LA / a8
--- RE = a. DO# = LA / a7
--- etc.
(Il s'agit évidemment de DO3 par rapport à LA3 ;
de D2 par rapport à LA2 =
LA3/2 ; etc.)
- De DO (440) = 440 / a9 et DO
(435) = 435 / a9
on tire que DO (435) / DO (440) = 435 / 440 ;
- De DO# (440) = 440 / a8 et DO (435) = 435
/ a8
on tire que DO# (435) / DO# (440) = 435 / 440 ;
- etc.
Autrement dit tous les nombres de la série 435 sont les nombres de la série
440 multipliés par un même facteur,
lequel facteur est 435/440. De même, tous les nombres de la série 415 sont les
nombres de la série 440 multipliés par un même facteur, lequel facteur est
415/400.
(1200/Log 2) Log (435/440) = -19,785 747 346 282 7 ~ - 20 points
(1200/Log 2) Log (415/440) = -101,270 624 748 447 ~ - 101 points
Choisir le diapason à 435 Hz (celui fixé en France par décret à l'époque romantique), c'est donc baisser tous les sons de l'échelle tempérée de 20 points vers le grave ; par rapport au diapason actuel qui fixe le la à 440 Hz et qui date de la fin du XIX° ou du début du XX° - congrès de Vienne et de Covent Garden - et qui par la suite a été normalisé par l'ISO en 1947 [date donnée sous réserve de confirmation]- Recommandation ISO 16).
Une gamme tempérée à l'actuel diapason dit baroque à 415 Hz,
c'est, par rapport à une gamme tempérée au diapason de 440 Hz, une gamme
translatée de 101 points vers le grave.
Comme on sait par les travaux de Félix
Savart qu'un écart de 1 point, notre oreille ne l'entend pas, cette gamme
tempérée dite baroque, en pratique, notre oreille va la confondre avec la gamme tempérée
baissée d'1 demi-ton vers le grave (le 1/2 ton étant de 100 points).
L'écart d'environ 0,3 Hz [ voir ci-après pour une examen plus précis] qu'on a sur chaque valeur de l'ambitus DO3/SI3 (entre
l'échelle obtenu par baisse d'1/2 ton - 100 points - et la valeur calculée
rigoureusement - baisse de 101 points) est donc négligeable, dans cette
plage de valeurs de fréquences.
Il paraît que les la de Conservatoire sont plus élevés
que le la normalisé.
(1200/Log 2) Log (442/440) = 7,851 415 040 126 5 ~
+ 8 points
(1200/Log 2) Log (444/440) = 15,667 383 390 535 5 ~
+ 16 points
(1200/Log 2) Log (445/440) = 19,562 174 794 920 8 ~
+ 20 points
Le la du Conservatoire peut donc être plus élevé d'un petit comma
(voir l'alinéa ci-après ; voir aussi, plus loin, le paragraphe sur les
diapasons).
Donnons les ordres de grandeur suivants, pour évaluer ces
écarts :
1/2 ton = 100 points ; 1/4 ton = 50 points ; 1/8 ton = 25 points ; 1 comma
= 20 à 24 points, selon sa nature.
Pouvoir discriminant de l'oreille = 4 points
(Un écart de 3 points, personnes ne l'entend ; un écart de 4 points, une
oreille fine peut tout juste le déceler).
En effet, en mémoire des travaux de Félix Savart, les
acousticiens ont donné son nom à l'intervalle le plus petit que l'oreille
humaine puisse déceler, et c'est à la 301ème & quelque partie de
l'octave, c'est-à dire un tout petit peu plus petit que la 300ème de l'octave
partie qui est 1200 / 300 = 4 points.
(Rappel : je dis et j'écris "1
point" - mot aisément compréhensible en français - là où la
littérature écrit (sans traduire) 1 cent, terme américain).
Revenons sur ce décalage de 101 points et examinons le de plus
près :
| a-b | a | b | (1200/Log 2)*(Log (a/b)) |
|
0,191 947 536 130 215 |
261,625 565 379 536 |
261,433 617 843 406 |
1,270 625 335 559 34 |
|
0,203 361 218 991 517 |
277,182 630 966 503 |
276,979 269 747 511 |
1,270 624 638 497 07 |
|
0,215 453 644 786 862 |
293,664 767 925 072 |
293,449 314 280 285 |
1,270 624 275 245 34 |
|
0,228 265 243 585 327 |
311,126 983 815 242 |
310,898 718 571 657 |
1,270 624 600 033 07 |
|
0,241 838 699 003 154 |
329,627 557 039 829 |
329,385 718 340 826 |
1,270 625 113 427 82 |
|
0,256 219 150 369 361 |
349,228 231 493 887 |
348,972 012 343 518 |
1,270 624 984 649 68 |
|
0,271 454 555 434 104 |
369,994 422 725 658 |
369,722 968 170 223 |
1,270 624 149 226 40 |
|
0,287 596 243 349 412 |
391,995 436 132 285 |
391,707 839 888 936 |
1,270 624 856 254 51 |
|
0,304 697 713 570 306 |
415,304 697 713 570 |
415,000 000 000 000 |
1,270 625 305 475 11 |
|
0,322 815 777 493 815 |
440,000 000 000 000 |
439,677 184 222 506 |
1,270 624 498 813 89 |
|
0,342 011 486 040 121 |
466,163 761 585 308 |
465,821 750 099 268 |
1,270 624 808 991 64 |
|
0,362 348 435 032 800 |
493,883 301 310 067 |
493,520 952 875 034 |
1,270 624 415 188 59 |
|
0,269 000
808 648 916 |
1,270 624
748 446 87 |
Le décalage en hertz, il augmente avec la fréquence, alors
que le décalage en points, il est constant
et reste autour de 1,270 625 points [les petits écarts autour de cette
valeur viennent peut-être d'arrondis de calcul, bien que ceux-ci aient été
faits avec Excel].
On peut faire un autre calcul : comparer 440 Hz et 440,5 Hz.
On trouve ceci : (1200/Log 2)*(Log (440,5 / 440)) = 1,966 194 474
904 96.
On peut donc retenir ceci : autour de 440 Hz, 1/2 Hz, c'est 2 points.
La
norme ISO 16 prescrit que le la3, fréquence internationale de référence,
c'est, à 20°C : 440 +- 0,5 Hz
Ainsi, +-2 points, c'est la précision de la fréquence de référence.
Retenons bien ceci car ça nous servira par la suite.
On peut aussi calculer les fréquences directement à partir du la. C'est facile puisque l'échelle est régulière (un barreau tous les 100 points).
|
x (multiplicateur) |
y |
|
Hz |
||
| a0 | 1, 000 000 000 | 0 |
la |
440 | |
| a1 | 1, 059 463 094 | 100 |
sib |
la# | 466, 163 761 36 |
| a2 | 1, 122 462 048 | 200 |
si |
493, 883 301 12 | |
| a3 | 1, 189 207 115 | 300 |
do |
523, 251 130 60 | |
| a4 | 1, 259 921 050 | 400 |
réb |
do# | 554, 365 262 00 |
| a5 | 1, 334 839 854 | 500 |
ré |
587, 329 535 76 | |
| a6 | 1, 414 213 562 | 600 |
mib |
ré# | 622, 253 967 28 |
| a7 | 1, 498 307 077 | 700 |
mi |
659, 255 113 88 | |
| a8 | 1, 587 401 052 | 800 |
fa |
698, 456 462 88 | |
| a9 | 1, 681 792 830 | 900 |
solb |
fa# | 739, 988 845 20 |
| a10 | 1, 781 797 436 | 1000 |
sol |
783, 990 871 84 | |
| a11 | 1, 887 748 625 | 1100 |
lab |
sol# | 830, 609 395 00 |
| a12 | 2, 000 000 000 | 1200 |
la |
880, 000 000 00 | |
|
x (diviseur) |
y |
|
Hz |
||
| a0 | 1, 000 000 000 | 0 |
la |
440 | |
| a1 | 1, 059 463 094 | - 100 |
lab |
sol# | 415, 304 697 72 |
| a2 | 1, 122 462 048 | - 200 |
sol |
391, 995 436 09 | |
| a3 | 1, 189 207 115 | - 300 |
solb |
fa# | 369, 994 422 71 |
| a4 | 1, 259 921 050 | - 400 |
fa |
349, 228 231 40 | |
| a5 | 1, 334 839 854 | - 500 |
mi |
329, 627 556 95 | |
| a6 | 1, 414 213 562 | - 600 |
mib |
ré# | 311, 126 983 80 |
| a7 | 1, 498 307 077 | - 700 |
ré |
293, 664 767 89 | |
| a8 | 1, 587 401 052 | - 800 |
réb |
do# | 277, 182 630 97 |
| a9 | 1, 681 792 830 | - 900 |
do |
261, 625 565 38 | |
| a10 | 1, 781 797 436 | - 1000 |
si |
246, 941 650 67 | |
| a11 | 1, 887 748 625 | - 1100 |
sib |
la# | 233, 081 880 80 |
| a12 | 2, 000 000 000 | - 1200 |
la |
220, 000 000 00 | |
Si on compare ce tableau aux précédents
(ch. 1, partie 2), on trouve qu'il donne exactement les mêmes résultats,
à condition d'arrondir à 6 ou 7 chiffres après la virgule les
résultats des calculs donnés par l'un et l'autre tableaux.
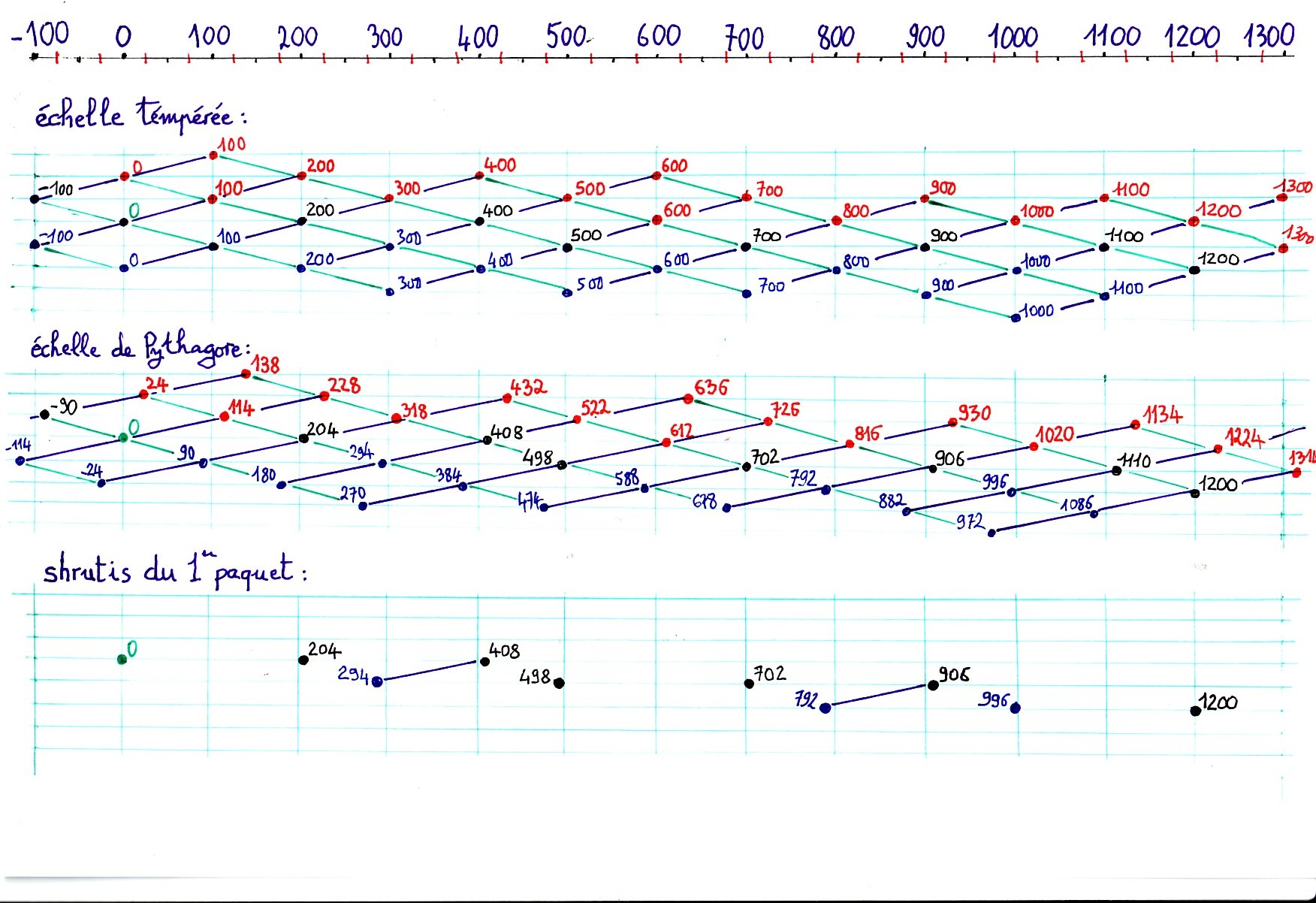
ANNEXE - ÉCHELLE TEMPÉRÉE ET ÉCHELLE PYTHAGORICIENNE NON TEMPÉRÉE
| -200 | -100 | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | 1300 | |||||||||||||||
| si## | ||||||||||||||||||||||||||||||
| si# | DO## | RE## | MI## | |||||||||||||||||||||||||||
| si | DO# | RE# | MI# | FA## | SOL## | LA## | SI## | |||||||||||||||||||||||
| sib | DO | RE | MI | FA# | SOL# | LA# | SI# | |||||||||||||||||||||||
| DOb | REb | MIb | FA | SOL | LA | SI | do# | |||||||||||||||||||||||
| DObb | REbb | Mibb | FAb | SOLb | LAb | SIb | do | |||||||||||||||||||||||
| FAbb | SOLbb | LAbb | SIbb | dob | ||||||||||||||||||||||||||
| dobb |

|
| -204 | 0 | 204 | 294 | 408 | 498 | 702 | 792 | 906 | 996 | 1200 | ||||||||||||||||||||
| *NI1 | SA | RI4 | GA4 | |||||||||||||||||||||||||||
| GA1 | MA1 | PA | DHA4 | |||||||||||||||||||||||||||
| DHA1 | NI1 | SA* | ||||||||||||||||||||||||||||