 |
***RaDio TEENTAAL***
L'
EVASION AUX SAVEURS INDIENNES !
|
| retour
à la page zéro
|
| Auteur |
Message |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Dim Mar 26,
2006 1:30 pm Sujet du
message: Kali & Durga Posté le: Dim Mar 26,
2006 1:30 pm Sujet du
message: Kali & Durga |
|
|
Pourquoi Kali, Durga et
Parvati ?
Un incident technique a fait perdre au forum
1 mois de données. Tout se passe donc comme si Kali
m'avait sabré 1 mois de travail.
Durga (= Kali sous un
autre aspect), Parvati puis Ganesh ont fait table rase de ce
que Kali avait détruit puis, intervenant chacun selon leurs
aptitudes propres (Parvati est la mère des arts & des
lettres, Ganesh un peu le père de la science et de la
technique), ils ont jeté les bases de la reconstruction en
proposant un plan.
Ce plan, c'est le récapitulatif de
ce que j'avais déjà publié pendant 1 mois, plus l'indication
de la marche à suivre pour aller au bout de l'exposé.
Tu es pressée, voici donc à quoi se résume le chapitre
9 : tu vois plus haut
le tableau des shrutis selon Nameeta Shah (tableau tiré de son
mémoire de fin d'études de l'université de Kanpur) : je les
ai groupés en paquets. Ca correspond à des réalités bien
précises et à des échelles musicales bien connues. Lesquelles,
pourquoi ? Pourquoi donc, en composition, on va plutôt choisir
tels sous-ensembles de shrutis plutôt que tels autres pour
créer un raga, quels effets produira-t' on si l'on sort de ces
ensembles : beau ? pas beau ? pourquoi ? J'espère que l'exposé
pourra donner des éléments de réponse de nature à initier
celui qui s'intéressera ou s'intéresserait à ces questions.
Comme tu es une lectrice pressée (et qui ne l'est pas
?), je te signale que dans les contributions où j'ai placé des
liens vers des sites internet qui donnent des extraits
musicaux, j'ai toujours indiqué la durée du morceau. C'est
fait pour faciliter au lecteur la gestion de son temps.
Bon dimanche.
Dernière édition par Veit le Ven Nov
03, 2006 12:44 am; édité 3
fois | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Dim Mar 26,
2006 2:06 pm Sujet du
message: La série 2^(i/12) Posté le: Dim Mar 26,
2006 2:06 pm Sujet du
message: La série 2^(i/12) |
|
|
La série 2^(i/12)
 Toonsia a donné hier
les bonnes valeurs pour les nombres de la série "2 puissance
(i/12)". Toonsia a donné hier
les bonnes valeurs pour les nombres de la série "2 puissance
(i/12)".
Voici les résultats
i = 00 ==>
1,000 000 000
i = 01 ==> 1,059 463 094
i = 02
==> 1,122 462 048
i = 03 ==> 1,189 207 115
i =
04 ==> 1,259 921 050
i = 05 ==> 1,334 839 854
i
= 06 ==> 1,414 213 562
i = 07 ==> 1,498 307 077
i = 08 ==> 1,587 401 052
i = 09 ==> 1,681 792
831
i = 10 ==> 1,781 797 436
i = 11 ==> 1,887
748 625
i = 12 ==> 2,000 000 000
Dans
Excel, il vous suffit d'écrire dans une cellule
=PUISSANCE(2;adresse de
la cellule voisine/12)
et dans la cellule voisine
vous tapez la valeur de i
Si vous tapez tous vos
chiffres de 0 à 12 dans une même colonne, de haut en bas, et
puis que la formule ci-dessus, vous la mettez dans une seconde
colonne à côté de la cellule où vous avez écrit 0, et que vous
faites recopier cette formule par Excel dans la 2ème colonne,
vous obtenez le résultat ci-dessus.
La valeur absolue
des fréquences, elle se déduit de cette échelle. C'est bête
comme chou. Prenez un point de départ à 261 Hz. Et faites vos
multiplications.
Ca vous donne une série de fréquences.
Poursuivez au-dessus en multipliant par deux les
fréquences trouvées.
Puis encore par en multipliant par
deux.
Revenez au début.. Poursuivez vers le bas en
divisant par deux.
Quelles limites dans ces
multiplications vers le haut et vers le bas ?
Il est prévu
qu'on en parle (revoir le plan, svp).
Fixer le point
de départ de l'échelle à 240 Hz ? Pas de souci. Allons-y !
Même méthode.
PAR CONTRE, VOUS OBSERVEREZ QUE LES
DEUX ENSEMBLES DE FRÉQUENCES QUE VOUS AUREZ AINSI CONSTRUITS
N' ONT AUCUN POINT COMMUN.
Et cela, c'est un résultat
capital : on a 2 univers parallèles et semblables mais
distincts et qui ne se mélangent jamais.
(A noter : Ici, on pourrait ouvrir
un point de discussion relatif à l'oreille
absolue)
Dernière
édition par Veit le Ven Nov 03, 2006 12:46 am; édité 1
fois | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Dim Mar 26,
2006 2:50 pm Sujet du
message: représentation graphique Posté le: Dim Mar 26,
2006 2:50 pm Sujet du
message: représentation graphique |
|
|
Représentation graphique de la série
2 ^(i/12)
D'abord, merci à Toonssia de
nous avoir introduit le symbole ^ pour signifier "puissance"
et pour montrer que le nombre qui suit le symbole ^ est un
exposant placé en haut et à droite du nombre qui précède ce
symbole. Car 2 ^(i/12) est plus commode à lire (à
l'oeil) que les mots "2 puissance (i/12)" ; mais à l'oreille
ça se dit pareil.
Ce qu'on cherche à faire, c'est à
placer sur la règle l'image des nombres de la série 2 ^(i/12),
pour i variant de 0 à 12, de 1 en 1. Allons-y !
 x = 2 ^(i/12) x = 2 ^(i/12)
 y = (1200 / Log 2)
* Log x y = (1200 / Log 2)
* Log x

y
= (1200 /
Log 2) * Log [2 ^ (i/12)]
= [1200 / Log 2] * [(i/12) * Log
2]
= 1200 *(i/12)
= (12 * 100) * (i / 12)
= 100 *
i
= 100 i
 L'image y, sur une
règle de 1200 points, de tout nombre x = 2 ^(i/12), c'est y =
100 i L'image y, sur une
règle de 1200 points, de tout nombre x = 2 ^(i/12), c'est y =
100 i
-- L'image de 2^(0/12) = 2^0 = 1, c'est 0,
c'est-à-dire une marque placée à l'origine de la règle ;
-- L'image de 2^(1/12) = c'est 100 points,
c'est-à-dire une marque placée à 100 points de distance de
l'origine de la règle ;
-- L'image de 2^(2/12) = c'est
200 points,
etc.
On continue à tracer sur notre
règle des marques espacées de 100 points en 100 points et jusqu'à l'extrémité de la règle :
-- L'image de
2^(12/12) = c'est 1200 points, et c'est l'extrémité de la
règle.
Si on prend un règle de 1,20 m (waoouh, la grande règle !),
1 point c'est 1mm.
Si on prend une règle de 30 cm (=
300 mm), elle est 4 fois plus petite :
- 1 point, ça
vaudra 1/4 mm ;
- 1 mm, ça exprimera 4 points
ET (cf.
ce que nous avons dit à propos du savart)
1 mm, à cette
échelle, ça représente ce que notre oreille -- si elle est
fine ! -- est capable de discerner.
Une conclusion
pratique pour nous, c'est que dans la suite de l'exposé, nous
ferons en sorte de travailler avec des nombres entiers de
points, en arrondissant à l'entier le plus proche les
résultats de calculs qui conduisent à exprimer un nombre de
points ; ce sera plus commode.
Avec cette échelle, 1
octave = 30 cm = 300 mm, notre série 2^(i/12) se représente
par des traits régulièrement espacés de 25 mm = 2,5 cm.
C'est cela, l'échelle chromatique tempérée relative !

Dernière édition par Veit le Ven Nov
03, 2006 12:47 am; édité 2
fois | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Lun Mar 27,
2006 2:12 am Sujet du
message: retour au plan Posté le: Lun Mar 27,
2006 2:12 am Sujet du
message: retour au plan |
|
|
retour au plan
A
ce stade de l'exposé, il est utile de relire le plan reçu de
Parvati :
5] en musique occidentale :
- l'échelle
chromatique tempérée
- l'échelle diatonique tempérée
-
nom des principaux intervalles
6]
- Quelques
théoriciens de la musique
- Un extrait des "Elémens de
musique", de d'Alembert (1752)
7] l'harmonium
8] en musique indienne :
- nom des notes de
l'échelle diatonique (les swaras)
- notion de tivra ;
notion de komal
9] relativité du diapason, référence
conventionnelle
- différents la ; différents do
10] relativité du sa, référence conventionnelle
11] échelles semblables, parallèles et décalées
(ça, on vient de le voir : c'est la remarque que je vous
ai écrite en lettres capitales d'imprimerie :
étant donnée la
suite 2^(i/12), si on l'applique à un DO de 261 Hz ou à un SA
de 240 Hz,
on obtient 2 ensembles de fréquences bien
distincts, qui n'ont aucun point commun mais qui sont
semblables).
 Tout ceci concerne
les échelles à tempérament égal; tant en musique occidentale
qu'en musique indienne (modern vibes) ; Tout ceci concerne
les échelles à tempérament égal; tant en musique occidentale
qu'en musique indienne (modern vibes) ;
les
échelles à tempérament inégal commenceront d'être étudiées à
la partie 12.  | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Mar Mar 28,
2006 12:21 pm Sujet
du message: 8 - 5 -1 Posté le: Mar Mar 28,
2006 12:21 pm Sujet
du message: 8 - 5 -1 |
|
|
5) mathématiques appliquées à la
musique
5.1)
l'échelle chromatique tempérée
tonique
DEFINITION :
tonique = point de départ d’une échelle
échelle chromatique tempérée
DEFINITION :
échelle chromatique tempérée =
suite de notes dont les fréquences sont 2^(i/12) fois la
fréquence de la tonique
(i étant un nombre entier auquel
on donne la valeur 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)
- La note de fréquence relative 2^(0/12] = 2^0 = 1 est
la tonique elle-même.
- La note de fréquence relative
2^(12/12] = 2^1 = 2 est la note à l’octave au-dessus de la
tonique ; elle est le point de départ de l’échelle au-dessus.
Formule d’Ellis :
On passe de toute hauteur relative (rapport de deux
fréquences), x, à la représentation de cette hauteur
relative, y, par la formule y = (1200 / Log 2) * Log x .
Ainsi, les barreaux l’échelle chromatique
tempérée sont disposés de la façon suivante : la tonique est
le zéro de l’échelle, et les autres barreaux sont aux cotes
100 points, 200 points, etc. jusqu’à 1100 points, le barreau
qui est à la cote 1200 points formant le zéro de la portion
supérieure de l’échelle (vers les aigus, donc).
Ceci en
montant car on peut aussi de même prolonger l’échelle vers le
bas (vers les graves) en plaçant un barreau tous les 100
points.
[Abus de
langage : 100 points, 900 points, 702 points ou autre valeur
exprimée en points – en « cents » dans ce que vous lirez chez
d’autres auteurs –, c’est, à proprement parler, une
représentation d’une hauteur relative. Cependant par abus de
langage, on simplifie et on dit « la hauteur ». Un autre abus
de langage est qu’on dit aussi bien « la hauteur »quand on
parle d’une hauteur absolue que quand on parle d’une hauteur
relative. Cette simplification facilite le discours et grâce
au contexte, on arrive à bien s’y retrouver car nous ne sommes
pas des ordinateurs !]
Remarquons :
a) la
régularité de cette échelle : les barreaux en sont
régulièrement espacés
(c’est à cause de cela qu’on dit
qu’il s’agit d’une échelle au tempérament égal –
Il existe
des tempéraments inégaux ; nous verrons cela plus tard) ;
b) que cette échelle est relative : on fixe la hauteur
de la tonique et hop cela nous détermine d’emblée tout un
ensemble de sons relatifs à cette tonique ;
c) tous
les sons qu’on se donne pour faire de la musique constituent,
dans cet univers, un
ensemble de sons formés par les sons de cette échelle qu’on
étend vers l’aigu et vers le grave en en multipliant les
fréquences par 2 et
en divisant les fréquences par 2 , autant de fois qu’on veut et
qu’on peut ;
d) jusqu'ici, nous n'avons nullement
donné de noms à des notes ; on est en dehors de toute
référence culturelle ; on est dans le pur domaine de la
physique et de la physiologie (l'acoustique et la
représentation des sons telle que la réalise l'ensemble formé
par notre oreille et notre cerveau ; enfin, plus exactement un
modèle de cette représentation).
notion de dièse ; notion de bémol
Dièse et bémol sont des qualificatifs utilisés
en musique occidentale pour désigner un barreau de l’échelle
par rapport au barreau voisin.
Soit « machin » le nom d’un
barreau :
« machin dièse », c’est le barreau au-dessus du
barreau « machin »
et
« machin bémol », c’est le
barreau au-dessous du barreau « machin »
notion de tivra ; notion de
komal
Tivra et komal sont des qualificatifs
utilisés en musique indienne pour désigner un barreau de
l’échelle par rapport au barreau voisin.
Soit « machin »
le nom d’un barreau :
« machin tivra », c’est le barreau
au-dessus du barreau « machin »
et
« machin komal »,
c’est le barreau au-dessous du barreau « machin »

Dernière édition par Veit le Lun Mai
01, 2006 11:29 am; édité 1
fois | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Mar Mar 28,
2006 3:09 pm Sujet du
message: 8 - 5 - 2 Posté le: Mar Mar 28,
2006 3:09 pm Sujet du
message: 8 - 5 - 2 |
|
|
5.2) emplacement des sillets d’une
guitare
L’emplacement des sillets d’une guitare
illustre bien les hauteurs relatives d’une échelle chromatique
tempérée.
En effet (& cela s’apprend au cours de
physique en classe de 2nde
- du moins c’était comme ça
dans les années soixante),
la fréquence de vibration d’une
corde vibrante est inversement proportionnelle à la longueur
de la corde
N.B.
Du point de vue historique, on retiendra que la découverte
date du XVII° et que l’assimilation de celle-ci date du XVIII°
; qu’il en est de même pour celle des logarithmes ; et que
cela est évidemment l’une des causes qui ont permis le
développement de la facture de la guitare aux XVIII°,
développement qui eut lieu d’abord en Espagne la
guitare y naquit au XVII°, du temps des échelles non
tempérées et la construction des guitares se développa au
XVIII° siècle après l'avènement de l'échelle tempérée.

Sur ma guitare, un instrument bon marché de
fabrication chinoise, qui sonne très bien et qui ressemble à
celui montré sur cette photo,
les sillets sont disposés de la façon suivante (cotes en
millimètres, par rapport au chevalet) :
- 00 : 650 (c’est le sillet de tête)
- 01 : 615 (la 1ère case est comprise entre le
sillet de tête, le n° zéro, et ce sillet n° 1)
-
02 : 580,5 (la 2ème case est comprise entre le
n° 1 et ce sillet n° 2)
- 03 : 548
- 04 : 517,5
- 05 : 488,5
- 06 : 461
- 07 : 435,5
- 08 : 411
- 09 : 388
- 10 : 366
- 11 : 346
- 12 : 327 (cette cote exprime aussi
l’emplacement du chevalet par rapport au bord de la
caisse)
- 13 : 308,5
- 14 : 291,5
- 15 : 275
- 16 : 259,5
- 17 : 245
- 18 : 231
- 19 : 219
L’origine
des cotes ci-dessus est le bord du chevalet, côté sillet de
tête.
La cote du sillet de tête est mesurée sur le bord de
ce sillet, côté chevalet.
La cote des différents sillets
est mesurée depuis l’origine jusqu’au bord intérieur de la
case délimitée par ce sillet.
La largeur d’un sillet est
de 2 mm.
Ainsi, le sillet 1 se trouve placé dans une
rainure dont les bords se trouvent à 613 et 615 mm du
chevalet.
On voit que le concepteur de l’instrument a
déterminé la position des sillets en considérant que le point
d’arrêt de la vibration de la corde se trouve sur l’arête
extérieure du sillet (extérieure par rapport à la case que
touche l’instrumentiste qui appuie de son doigt sur la corde).
En effet : 327-2 = 325 et 325 = 650 / 2.
(N.B. C'est facile de deviner où
sont les points d'arrêts de la vibration d'une corde de
guitare, car les sillets sont minces et triangulaire la
section du chevalet, mais sur une veena qui a un chevalet
plat...  ) )
Dans l'hypothèse
que nous venons de faire quant à la position des points
d'arrêt de la vibration de la corde, il vient que nous devons
retenir la suite de nombres que voici (on enlève partout 2 mm,
sauf à la cote du sillet de tête, vu comme les mesures ont été
prises) :
650
613
578,5
546
515,5
486,5
459
433,5
409
386
364
344
325
306,5
289,5
273
257,5
243
229
217
En divisant 650 (longueur de la corde à vide)
par chacun de ces nombres, on obtient la série :
1,000 000 000 (corde à vide)
1,060 358
891
1,123 595 506
1,190 476 190
1,260 911 736
1,336 073 998
1,416 122 004
1,499 423 299 (=
pratiquement 1,5)
1,589 242 054
1,683 937 824
1,785 714 286
1,889 534 884
2,000 000 000 (corde
pressée sur la 12 ème case)
2,120 717 781
2,245 250
432
2,380 952 381
2,524 271 845
2,674 897 119
2,838 427 948
2,995 391 705 (= presque 3)
Reprenons notre série
des valeurs de 2^(i/12)
calculée pour i variant de 0 à
12,
faisons les calculs pour i variant de 13 à 19 et comparons.
1,000 000 000<== i = 00 ==>1,000 000 000
1,059 463 094<== i = 01 ==>1,060 358 891
1,122 462 048<== i = 02 ==>1,123 595 506
1,189 207 115<== i = 03 ==>1,190 476 190
1,259 921 050<== i = 04 ==>1,260 911 736
1,334 839 854<== i = 05 ==>1,336 073 998
1,414 213 562<== i = 06 ==>1,416 122 004
1,498 307 077<== i = 07 ==>1,499 423 299
1,587 401 052<== i = 08 ==>1,589 242 054
1,681 792 831<== i = 09 ==>1,683 937 824
1,781 797 436<== i = 10 ==>1,785 714 286
1,887 748 625<== i = 11 ==>1,889 534 884
2,000 000 000<== i = 12 ==>2,000 000 000
2,118 926 189<== i = 13 ==>2,120 717 781
2,244 924 097<== i = 14 ==>2,245 250 432
2,378 414 230<== i = 15 ==>2,380 952 381
2,519 842 100<== i = 16 ==>2,524 271 845
2,669 679 708<== i = 17 ==>2,674 897 119
2,828 427 125<== i = 18 ==>2,838 427 948
2,996 614 154<== i = 19 ==>2,995 391 705
On trouve de
petits écarts, mais j'ai fait mes mesures avec un mètre
ordinaire qui mesure au millmètre près et les cotes trouvées
au 1/2 mm, elles sont estimées (je n'ai pas les moyens de
réaliser des mesures précises au 1/10ème de mm près !).
Appliquons la formule d'Ellis à chacune des deux
séries et voyons ce que l'on trouve. Pour la série bleue, on
peut se dispenser de faire les calculs, étant donnée comme on
l'a construite. On n'a donc les calculs à faire que sur la
série rouge. Avec Excel, ça va beaucoup plus vite qu'à la
machine à calculer !... Et on trouve ceci :
0000<== i = 00 ==>0000,000 000 0
0100<== i = 01 ==>0101,463 173 6
0200<== i = 02 ==>0201,747 311 2
0300<== i = 03 ==>0301,846 519 7
0400<== i = 04 ==>0401,360 748 4
0500<== i = 05 ==>0501,599 895 8
0600<== i = 06 ==>0602,334 677 0
0700<== i = 07 ==>0701,289 269 9
0800<== i = 08 ==>0802,006 650 2
0900<== i = 09 ==>0902,206 644 9
1000<== i = 10 ==>1003,801 522 0
1100<== i = 11 ==>1101,637 384 0
1200<== i = 12 ==>1200,000 000 0
1300<== i = 13 ==>1301,463 173 0
1400<== i = 14 ==>1400,251 644 0
1500<== i = 15 ==>1501,846 520 0
1600<== i = 16 ==>1603,040 743 0
1700<== i = 17 ==>1703,380 085 0
1800<== i = 18 ==>1806,110 544 0
1900<== i = 19 ==>1899,293 611 0
On calcule
aisément que l'écart moyen de des nombres de la série rouge,
par rapport à leurs homologues de la série bleue, est
inférieur à 0,31%, que cet écart est compris entre 1,46% (sur
le 1er sillet) et de -0,04 % sur le dernier sillet.
On
observe aussi que, sauf sur le 18ème sillet où l'écart est de
6 points, celui-ci est toujours inférieur à 4 points.
Sur
20 sons produits par chaque corde (en vibration simple, sans
effets) :
-- 1 son s'écarte de 6 points de l'échelle
chromatique tempérée théorique,
-- pour 3 sons, l'écart
est inférieur à 4 points (mais supérieur à 3),
-- pour 3
sons, l'écart est inférieur à 3 points (mais supérieur à 2),
-- pour 9 sons, l'écart est inférieur à 2 points (mais
supérieur à 1),
-- pour 1 son, l'écart est inférieur à 1
point (mais supérieur à 0, c-à-d. positif),
-- pour 2 sons
(la corde à vide et son octave), l'écart est nul,
-- pour
1 son, l'écart est inférieur à 1 point, mais dans l'autre
sens.
 Cette guitare mérite
la récompense qu'elle a obtenue : un diapason d'or ! Cette guitare mérite
la récompense qu'elle a obtenue : un diapason d'or !
(C'est marqué sur une étiquette collée au fond de sa
caisse !)
 Luthiers en herbe que
vous êtes désormais devenus, je vous laisse le soin de
calculer l'influence d'un écart de 1/2 mm sur la position d'un
sillet... Luthiers en herbe que
vous êtes désormais devenus, je vous laisse le soin de
calculer l'influence d'un écart de 1/2 mm sur la position d'un
sillet...
De plus,
vous observerez que ces considérations théoriques, elles sont
valables pour tout instruments à cordes, frettés (= à sillets)
ou non (pour un instrument sans sillets, tel que le violon par
exemple, le point d'arrêt de la vibration de la corde, il est
sous le doigt du musicien, l'autre point d'arrêt étant au
chevalet)
| |
 |
Nandini
Teentaalien senior

Inscrit le: 03 Mar
2006
Messages: 59
|
 Posté le: Mer Mar 29,
2006 2:47 pm Sujet du
message: Posté le: Mer Mar 29,
2006 2:47 pm Sujet du
message: |
|
|
Luthier ??      
Mon père est
maître luthier. Il fabrique des instruments de musique ou fait
des réparations (luths, violons..). Il donne aussi des cours
!!!
Je vais lui montrer tout ça, parce que j'ai
vraiment l'impression que c'est impossible à comprendre, tout
cela !!! | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Jeu Mar 30,
2006 1:22 am Sujet du
message: du luthier Posté le: Jeu Mar 30,
2006 1:22 am Sujet du
message: du luthier |
|
|
Ah ! Ton papa te résumera
tout ça en 1 formule, voire quelques tableaux, Nandini !  Et
ce que j'explique là n'est qu'une toute petite toute petite
partie de son métier ! Et
ce que j'explique là n'est qu'une toute petite toute petite
partie de son métier !
La connaissance des bois, l'art
des collages, le savoir faire avec les vernis, l'estimation
des forces en présence (sur un cadre de piano : des tonnes !
et la force de traction des cordes sur un manche de guitare,
c'est un bon paquet de kilo), des notions de mécanique,
d'acoustique, de musique.... plus le sens du client, de ses
goûts, de son style, savoir prévenir ses attentes, ses
non-dits, le respecter et lui donner le moyen de sublimer son
chef-d' oeuvre (l'instrument) sans l'étouffer, sans rien lui
imposer... Savoir jongler avec les chiffres pour tenir la
comptabilité du magasin, connaître un peu la législation,
recevoir les clients, les dénicher, les fidéliser... voilà
comme je vois le métier de ton papa, Nandini, et c'est un beau
métier !
 Et tant mieux si cet
exposé suscite un dialogue entre père et fille ! Et tant mieux si cet
exposé suscite un dialogue entre père et fille !
Il y
a quelques points cependant sur lesquels je veux attirer ton
attention :
1) jusqu'ici, on n'est qu'à la moitié de
l'exposé et, en résumé, on a fait 2 choses : on a rappelé des
bases de maths et on a introduit l'échelle chromatique
tempérée ;
2) je n'ai pas dit pourquoi elle est
intéressante et ce qu'elle offre comme avantages par rapport
aux échelles non tempérées, car cela tu le liras partout ;
c'est dans tous les exposés classiques ;
3) dans la
suite, le rapport de 2 entre 2 fréquences ayant déjà été dit
comme le plus consonant, on parlera d'échelles non tempérées,
celle dite de Pythagore (on introduit le nombre 3) et celle
dite d'Aristoxène (on introduira le nombre 5).
4)
L'ensemble des 22 shrutis apparaît comme une combinaison de
notes prises dans ces deux échelles, plus un Ni qui est à
part.
5) Ton père te parlera peut-être de l'échelle de
Zarlino. C'est un autre nom de l'échelle dite d'Aristoxène (on
l'appelle échelle d'Aristoxène-Zarlin). Je dirais un mot de
l'intérêt de ces échelles (solfèges, consonances).
6)
Mon exposé, c'est un synthèse d'autodidacte de quantités de
choses lues sur le sujet, crayon et papier en main, depuis des
années. Il se limite donc nécessairement à des principes
théoriques très simples.
7) Mon exposé, il est un peu
long car j'essaye de justifier chaque chose pour quelqu'un qui
démarre l'étude du sujet à partir de rien. J'essaye aussi de
ne jamais employer une notion sans l'avoir définie auparavant.
Donc, reprends le à tête reposée, prends le temps, vas-y
doucement, ne cherche pas au delà de ce qui est marqué ;
quelquefois même lis en diagonale pour saisir l'essentiel et
tu verras, tu devrais comprendre sans souci !
 Au
moins, ça devrait à tous vous donner des bases pour assimiler
vite les articles que vous trouveriez sur le sujet dans vos
encyclopédies voire sur le net (mais attention ! là,
évidemment, il y a du bon et du moins bon !) Au
moins, ça devrait à tous vous donner des bases pour assimiler
vite les articles que vous trouveriez sur le sujet dans vos
encyclopédies voire sur le net (mais attention ! là,
évidemment, il y a du bon et du moins bon !)
9) Bien
sûr, quand l'exposé sera terminé, si ton papa voulait nous
livrer des choses bonnes à savoir (et notamment sur les
instruments à vent --- plus compliqués à opprendre que les
instruments à corde) ce serait avec plaisir qu'on l'entendrait
!  | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
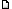 Posté le: Jeu Mar 30,
2006 1:45 am Sujet du
message: bending Posté le: Jeu Mar 30,
2006 1:45 am Sujet du
message: bending |
|
|
Avant de donner le nom des
notes et de définir les principaux intervalles,
et parce que
j'en ai parlé dans ma réponse à Rose des vents mardi, je vais
vous dire de suite un petit mot sur le bending
Bending = un effet de
jeu, à la guitare, tel que voici.
L'instrumentiste,
étendant le doigt qui appuie une corde sur la touche, ou, plus
généralement le pliant en le ramenant vers le creux de sa
paume, translate le point de contact de la corde sur le sillet
qui arrête la vibration de celle-ci.
Que se passe-t-il
?
--> La longueur de corde est augmentée. En effet,
depuis le point de contact de la corde avec le chevalet, on
peut imaginer un triangle rectangle fictif dont le petit côté
est un segment de chevalet, l'hypothénuse la corde dans sa
position déplacée et le grand côté la corde dans sa position
d'origine. L'hypothénuse étant plus grande que le grand côté,
la longueur vibrante de la corde est bien plus grande.
Augmentation de la longueur de corde ==> tendance à un
son plus grave.
--> La tension de la corde est
augmentée.
Augmentation de la tension de la corde ==>
tendance à un son plus aigu.
Quel est celui des deux
phénomènes qui l'emporte ?
Le son monte vers l'aigu
(légèrement, mais distinctement) quand l'instrumentiste écarte
la corde de sa position d'origine, en la faisant glisser le
long du sillet. La fréquence du son augmente continûment, puis
revient à sa fréquence de départ si l'instrumentiste remet la
corde dans sa position de départ.
Cette variation de
fréquence est inférieure au 1/2 ton
[1/2 ton =
l'intervalle entre les sons produits par la même corde touchée
sur 2 cases voisine]. | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
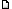 Posté le: Sam Avr 01,
2006 3:10 pm Sujet du
message: 8 - 5 -3 Posté le: Sam Avr 01,
2006 3:10 pm Sujet du
message: 8 - 5 -3 |
|
|
5.3) nom des degrés de
l'échelle
Dans la littérature, au lieu de
parler de "barreaux de l'échelle", comme on a fait jusqu'à
présent, on parle de "degrés de l'échelle" (alors que dans le langage courant
on parle de degrés d'un escalier). On doit admettre ce
fait et faire avec car il est impossible d'aller contre.
Dans ce paragraphe-ci, on va donner les noms des
degrés de l'échelle en musique occidentale. Les noms des
degrés de l'échelle en musique indienne seront donnés après la
page qui parlera de l'harmonium.
Par définition,
DO = le
zéro de l'échelle
RE = la
marque à 200 points au dessus du zéro
MI = la
marque à 400 points au dessus du zéro
FA = la
marque à 500 points au dessus du zéro
SOL = la
marque à 700 points au dessus du zéro
LA = la
marque à 900 points au dessus du zéro
SI = la
marque à 1100 points au dessus du zéro
Et on
recommence à DO à 1200 points pour l'échelle suivante.
Cette échelle ascendante, on l'appelle diatonique.
On
l'appelle tempérée car
c'est un sous-ensemble de l'échelle chromatique dont chaque
degré est distant de 100 points de chacun des degrés voisins.
Les autres degrés de l'échelle chromatique (i.e. ceux
qui ne font pas partie de l'échelle diatonique), on les
baptise en ayant recours aux notions de dièse et bémol.
--> la marque à 100 points au dessus du zéro = RE b
= DO #
--> la marque à 300 points au dessus du zéro =
MI b = RE #
--> la marque à 600 points au dessus du
zéro = SOL b = FA #
--> la marque à 800 points au
dessus du zéro = LA b = SOL #
--> la marque à 1000
points au dessus du zéro = SI b = LA #
4 notes de
l'échelle diatonique peuvent être appelées d'un 2ème nom :
--> DO = SI#
--> MI = FAb
--> FA = MI#
--> SI = DOb
Remarquons bien :
- que
jusqu'ici, nous n'avons pas fixé de hauteur absolue ni au do
ni à aucune des notes ;
- que, l'échelle chromatique étant
donnée, si on fixe la hauteur (la fréquence) d'une seule note
de l'échelle, alors s'en déduit la fréquence de toutes les
autres. | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Jeu Avr 06,
2006 12:58 am Sujet
du message: 8 - 5 - 4 - a Posté le: Jeu Avr 06,
2006 12:58 am Sujet
du message: 8 - 5 - 4 - a |
|
|
5.4) noms des principaux
intervalles
Voici les noms des principaux
intervalles :
(attention
! les définitions qui suivent seront assouplies juste après
qu'elles auront été données)
- SECONDE MINEURE
= 100 points
- SECONDE MAJEURE = 200 points
Pourquoi mineure et majeure ?
Ca vient du latin :
- minus = plus
petit
- major[i] = plus
grand
- TIERCE MINEURE = 300 points
- TIERCE
MAJEURE = 400 points
- Seconde ? Tierce ? Pourquoi ces
noms ?
Parce qu'on compte ainsi :
a) do et ré, par
exemple, sont deux notes adjacentes de l'échelle diatonique.
De ce fait on dit que l'écart entre ces deux notes (une et
deux) est une seconde. C'est une seconde grande car il existe
une seconde petite
- la grande étant plus grande que
la petite, on l'appelle majeure ;
- la petite étant plus
petite que la grande, on l'appelle mineure.
b) do et ré bémol, par exemple,
sont deux notes adjacentes de l'échelle chromatique, et de
noms différents (à l'altération près).
Aussi on dit que
l'écart entre ces deux notes est une seconde. Et c'est une
seconde petite.
Un écart entre deux notes de
adjacentes de l'échelle chromatique et de même nom, à
l'altération près (par exemple entre do et do dièse), on ne
lui donne pas le nom de seconde mineure bien qu'il vaille
aussi 100 points si l'échelle considérée est l'échelle chromatique tempérée. Cela vient d'habitude de langage prises
du temps des échelles non tempérées, avant que la convention
d'adopter l'échelle tempérée ne s'installe peu à peu (disons
en gros et pour fixer les idées, entre 1650 et 1750 en
Europe).
- Exemple de tierce majeure : do / mi.
(do, ré, mi font 3 notes et l'intervalle entre do et mi
est de 400 points)
- Exemple de tierce mineure : la /
do.
(il s'agit ici du do juste au-dessus du si qui est
au-dessus du la considéré ;
la, si, do font 3 notes et
l'intervalle entre la et do est de 300 points)
On
donne les exemples en montant, mais on pourrait aussi bien
prendre des exemples en descendant :
-- ré / do & mi /
ré sont des secondes majeures,
-- fa / mi est une seconde
mineure ;
-- fa / ré est une tierce mineure ;
-- fa /
ré b est une tierce majeure.
- QUARTE = 500 points
-- Exemples :
--- en montant : do / fa.
--- en
descendant : do / sol
(ce n'est pas du même do qu'il
s'agit, dans ces deux exemples)
On compte bien do, ré, mi,
fa = 4 notes (et 500 points de do à fa en montant).
On
compte bien do, si, la, sol = 4 notes (et 500 points de do à
sol en descendant).
- QUARTE AUGMENTÉE = 600
points
-- exemple : do / fa#
- QUINTE = 700
points
-- Exemples :
--- en montant : do / sol.
--- en descendant : do / fa
(ce n'est pas du même do
qu'il s'agit, dans ces deux exemples)
On compte bien do,
ré, mi, fa, sol = 5 notes (et 700 points de do à sol en
montant).
On compte bien do, si, la, sol, fa = 5 notes (et
700 points de do à fa en descendant).
- SIXTE =
900 points
-- Exemple : do / la
- SEPTIÈME =
1100 points
-- Exemple : do / si
- OCTAVE =
1200 points
-- Exemple : do / do
(do, ré, mi, fa, sol,
la , si, do = 8 notes sur l'échelle diatonique)
-
NEUVIÈME = 1200 + 200 = 1400 points
-- Exemple : do / ré
(il s'agit du ré juste au-dessus du do qui est à l'octave
du do de départ)
- DOUZIÈME = 1200 + 700 = 1900
points
-- Exemple : do / sol
(il s'agit du sol qui est
à la quinte du do qui est à l'octave du do de départ)
- OCTAVE REDOUBLÉE = 1200 + 1200 = 2400 points
-- Exemple : do / do
(le 2ème do est à la double
octave du do de départ ;
la fréquence de ce 2ème do vaut 4
fois la fréquence du do de départ )
- DIX-SEPTIÈME
= 2400 + 400 = 2800 points
-- Exemple : do / mi
(ce mi
est le mi qui est à la tierce majeure de la double octave du
do de départ)
SVP, faites-vous même l'exercice de
compter les notes sur la grande échelle diatonique pour ien
vous persuader des noms des grands intervalles (prenez modèle
sur ce que je vous ai indiqué pour les intervalles plus
petits). Ce que j'appelle ici la "grande échelle diatonique",
ce n'est qu'une suite d'échelles diatonaiques semblables mises
bout à bout.
Dernière
édition par Veit le Jeu Avr 06, 2006 9:23 pm; édité 1
fois | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Jeu Avr 06,
2006 9:21 pm Sujet du
message: 8 - 5 - 4 - b Posté le: Jeu Avr 06,
2006 9:21 pm Sujet du
message: 8 - 5 - 4 - b |
|
|
|
Les définitions qu'on a
donné hier étaient provisoires car elles avaient pour but de
faire comprendre, pour chacun des intervalles considérés la
notion correspondante et de donner l'explication du nom des
intervalles.
En fait, le nombre de notes qu'on compte
sur l'échelle diatonique entre les bornes de l'intervalle,
celles-ci comprises, il est important ; et aussi il est
important que la valeur de l'intervalle soit la valeur que
l'on a donnée hier OU PROCHE DE
CELLE-CI.
Disons pour fixer les idées
(peut-être devrons-nous revoir cela par la suite ?)
à plus
ou moins 1 comma, quel que soit l'intervalle considéré.
Ainsi, nous avons assoupli la définition des
intervalles et c'est important pour la suite (sinon, nous
aurions été gênés dans la suite, lors de l'étude des échelles
non tempérées).
Discuter et choisir la meilleure
valeur des intervalles, c'est, au fond, ainsi que se résume
l'objet de notre propos.
Qu'est-ce qu'un comma ? Il en
existe plusieurs, qui ont chacun leurs noms.
Mais pour les
besoins de notre exposé !
1 comma = tout intervalle compris
entre 20 et 24 points
Il existe des intervalles
plus petits que le comma mais pour ce chapitre nous n'aurons
pas besoin de connaître leurs noms.
Voyons maintenant
les noms d'intervalles plus grands.
1 ton = 200
points (ou environ)
1/2 ton =
100 points (ou environ)
1/4
ton = 50 points (ou environ)
1/8
ton = 25 points (ou environ)
Attention
! Comme la théorie de la musique a été étudiée
bien avant l'avènement de l'échelle tempérée, le vocabulaire
du solfège en a gardé des traces, et c'est pourquoi 2 notes
qui, dans l'échelle tempérée, correspondent à la même hauteur
de son mais n'ont pas le même nom ne sont pas confondues mais
dites "enharmoniques".
En pratique, on doit faire
attention aux noms qu'on donne aux notes et il y a un tas de
règles pour cela, que je trouve compliquées. Un des buts de ce
chapitre, c'est ausi de trouver les choses simples qui sont à
la base de ces règles et dont, par conséquent, ces règles vont
découler naturellement.
(Vous irez svp voir votre cours de
solfège pour en prendre connaissance !).
Une autre
conséquence, c'est que, bien que dans l'échelle chromatique
tempérée (la seule qu'on nous apprenne à l'école), tous les
demi-tons ont même valeur (100 points), on les distingue par
leur nature :
- le 1/2
ton diatonique (ce sont par exemple do / si et
mi / fa ;
et ces mêmes intervalles dans l'autre sens ;
mais aussi sol / fa#, par exemple)
- le 1/2 ton
chromatique (par exemple fa / fa# et si / si b).
Quand nous passerons à l'étude des échelles non
tempérées, nous verrons que dans de telles échelles ces 1/2
tons n'ont pas la même valeur.
Dernière édition par Veit le Ven Nov
03, 2006 12:59 am; édité 1
fois
| |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Sam Avr 08,
2006 1:37 am Sujet du
message: pause Posté le: Sam Avr 08,
2006 1:37 am Sujet du
message: pause |
|
|
O.K. On a bien travaillé !

Faisons une petite pause, puis on reprendra par une brève
parenthèse d'histoire. | |
 |
Miss_Diey
Teentaalien VIP


Inscrit
le: 27 Aoû 2005
Messages: 1540
Localisation:
Marseille
|
 Posté le: Sam Avr 08,
2006 1:21 pm Sujet du
message: Posté le: Sam Avr 08,
2006 1:21 pm Sujet du
message: |
|
|
cela voudrait dire que fa#
est à la fois 1/2 ton diatonique et 1/2 ton chromatique 
_________________
Today:
I'm Diey Akhsay Kumar 
My skyblog:
http://bollymania.skyblog.com/ | |
 |
Veit
Teentaalien confirmé


Inscrit le: 25 Nov
2005
Messages: 409
Localisation: Tremblay (93)
|
 Posté le: Sam Avr 08,
2006 2:12 pm Sujet du
message: fa# Posté le: Sam Avr 08,
2006 2:12 pm Sujet du
message: fa# |
|
|
Non, Miss Diey.
Fa#, c'est une marque sur l'échelle, l'origine de
celle-ci ayant été fixée
(fixée à Do, dans tout ce que
nous avons considéré jusqu'à présent).
Le 1/2 ton,
c'est un intervalle entre une note et une autre.
Si
fa# est l'une des 2 bornes de l'intervalle, on aura :
---> fa# / fa = 1/2 ton chromatique ; fa / fa # en
est un aussi ;
---> fa# / sol = 1/2 ton diatonique
; sol / fa # en est un aussi.
Bises | |
 |
|
































