***RaDio TEENTAAL***

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Nous avons défini ainsi l'intervalle entre le la et le do :

900 points

Par la suite, nous verrons 2 autres intervalles possibles et leur justification :

27/16 (= 906 points)

5/3 (= 884 points)

La hauteur du la étant fixée, cela nous donne 3 hauteurs possibles pour le do.

Si on choisit un la de départ et un intervalle la / do, alors, si on cherche la en se servant des 2 autres intervalles considérés, on trouvera 2 autres valeurs pour le la !

Comme, donc, on a do point de départ flottant et plusieurs façons de considérer les choses, il y a matière à discussion et ça fait des siècles qu'elle dure !

En somme, la situation est la suivante, en Occident :
- l'échelle chromatique tempérée est la seule enseignée dans les écoles ;
- le solfège est basé sur l'échelle dite de Pythagore (où l'intervalle de do à la est égal à 27 / 16) ;
[nous appellerons cette échelle : "échelle pythagoricennne"]
- c'est l'échelle d'Aristoxène-Zarlin (où l'intervalle de do à la est égal à 5 / 3) qu'on trouve dans la plupart des encyclopédies, au début des articles généraux consacrés à la musique
[Olivier Bettens dit que Zarlino s'est basé sur les travaux de Ptolémée ; cependant c'est sous le nom de "échelle d' Aristoxène-Zarlin qu'on la connaît", et aussi sous le nom de "échelle des physiciens"]. Nous la désignerons par le nom : "échelle harmonique", plus simple.
Ces échelles sont présentées en détail par la norme française NF S 30-107 (acoustique - vocabulaire de l'acoustique musicale) de décembre 1972.
On peut acheter cette norme à l'AFNOR [ http://www.afnor.org ].

On choisira comme on veut ce la de départ : cf. ce qui a été dit plus haut sur les valeurs variées du diapason selon les lieux et le temps, et en vertu du principe de liberté quant à l'application des normes, aux risques & périls des minoritaires qui s'en écartent si la norme est largement appliquée.

On remarquera ceci : [27/16] / [5/3] = [81/80].

Ce rapport de 81/80 s'appelle le comma syntonique

Nous le retrouverons dans la suite de l'exposé.

Remarquons aussi que :
440 / (81/80) = 434,567 901 234 568
qu'on peut arrondir à 434,57 (1er arrondi)
mais qu'on peut arrondir aussi à 435 (2ème arrondi),
selon ce qu'on veut faire (cf. les indications de précision fournies par la norme ISO 16).

Il vous sera facile de calculer les fréquences de do en partant d'une hauteur de la que vous aurez choisie, lorsque les intervalles la / do sont exprimés par des fractions.

Mais quand il est donné en nombre de points ?

Pour la valeur 900 points, on peut retourner à la définition [ rappelez-vous, c'était 2^(9/12)]. On peut aussi la calculer en se souvenant que la fonction exponentielle, c''est la fonction inverse de la fonction Logarithme, ce qui nous donne une méthode pour calculer le rapport entre 2 fréquences, pour tout intervalle que l'on considère sur notre règle.

y = Log x
x = e^y
==>
e^Log x = x

Notons LN (x) pour désigner Log (x) et EXP (y) pour désigner e^y
(c'est ainsi qu'il faut faire dans Excel).
Nous avons donc : EXP [LN (x) ] = x

(J'écris des crochets et des parenthèses pour rendre la lormule plus lisible, mais dans Excel, il vous faudra mettre des parenthèses partout et pas de crochets, pas de blancs non plus).

Alors la formule d'Ellis s'écrit :
formule d'Ellis : y = [1200 / LN (2)] * LN (x)

Il vient donc : y / [1200 / LN '2)] = LN (x)
et donc :
EXP ( y / [1200 / LN (2)] ) = EXP [LN (x)] = x

Autrement dit, la formule réciproque de la formule d'Ellis est :
formule réciproque de la formule d'Ellis : x = EXP ( y / [1200 / LN (2)] )

exemple :
si y = 900, x vaut :
x = EXP ( 900 / [1200 / LN (2)]) = 1,681 792 830 507 43

à comparer à :
PUISSANCE(2;(9/12)) = 1,681 792 830 507 43

et à :
27 / 16 = 1,687 5

ainsi qu'à :
5 / 3 = 1,666 666 666 666 66...

Si on choisit comme échelle de référence, au lieu de l'échelle chromatique tempérée, l'échelle pythagoricienne, alors on passera à l'échelle harmonique en baissant les notes d'un ou plusieurs commas syntoniques.

Si on choisit comme échelle de référence, au lieu de l'échelle chromatique tempérée, l'échelle harmonique, alors on passera à l'échelle pythagoricenne en montant les notes d'un ou plusieurs commas syntoniques.

Nous verrons cela dans la suite de l'exposé.

Les facteurs d'instruments de musique font comme ils veulent.
Les compositeurs aussi.
_________________
"Les détails font la perfection.
La perfection n'est pas un détail"
Léonard de Vinci

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Partant d'un do,
nous avions annoncé 3 valeurs possibles pour le la.

De même, partant d'un SA,
nous avons 3 valeurs possibles pour le DHA
puisque Nameeta Shah nous donnait :

DHA3 : 884 ( 5/3)
DHA4 : 906 (27/16)

et que nous avions défini, pour fixer les idées, le DHA comme étant à 900 points au-dessus du SA.

Tout se passe comme si les shrutis en musique indienne existaient du fait de la coexistence de l'échelle pythagoricienne et de l'échelle harmonique sans qu'il y ait recherche de faire primer l'une sur l'autre. Les deux ont leur raison d'être et sont admises.

Par contre, le système occidental aura cherché une solution moyenne, le tempérament (vous en trouverez les causes expliquées dans tous les livres, ce sont toujours les mêmes : faciliter les transpositions, faciliter le jeu en commun d'ensembles instrumentaux de plus en plus vastes). Je suis convaincu que c'est le tempérament égal qui a facilité la fabrication des grands orgues et la naissance des symphonies au XVIII°, puis des grands orchestres au XIX°). Et tout cela, au fond, grâce à la découverte des logarithmes par Neper au début du XVII°.

Il y aussi, parmi les causes, des différences de mentalité entre l'orientale et l'occidentale.

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Elémens de musique théorique et pratique, Paris 1752, page 45, note u :

Tous les demi-tons étant égaux dans le tempérament que monsieur Rameau propose, il s'ensuit que les douze demi-tons ut, ut #, ré, ré #, mi, mi #, et cetera formeront une progression géométrique continue, c'est-à-dire, une suite dans laquelle ut sera à ut # dans le même rapport que ut # à ré, que ré à ré #, et cetera et ainsi de suite.

Ces douze demi-tons sont formés par une suite de treize sons dont UT et son octave ut sont le premier et le dernier. Ainsi pour trouver par le calcul la valeur de chaque son dans le tempérament dont il s'agit, la question se réduit à trouver entre les nombres 1 et 2 onze autres nombres qui fassent avec 1 et 2, une progression géométrique continue.

Pour peu qu'on ait l'usage du calcul, on trouvera facilement chacun de ces nombres, ou du moins sa valeur approchée. En voici l'expression que les Mathématiciens reconnoîtront facilement, et que les autres peuvent passer.

http://www.music.indiana.edu/tfm/18th/ALEMEL_01GF.gif

Le texte intégral des "Elémens de musique théorique et pratique", manuel publié à Paris en 1752 est ici :
http://www.music.indiana.edu/tfm/18th/ALEMEL_TEXT.html
L'édition originale comporte 172 pages.

Je possède un fac-similé de l'exemplaire de la bibliothèque de Genève,
édité en 1982 par Slatkine Reprints, épuisé chez l'éditeur
mais que mon libraire a pu dénicher !

L'auteur de ce manuel, c'est d'Alembert.
Le manuscrit a été approuvé par Condillac le 23 novembre 1751.

Sur mon fac-similé, la lettre t manque au mot "éléments".
Ecrire "élémens" n'est pas une faute de recopie de ma part./i]

Vous trouverez cette note u à la fin de la copie disponible sur internet.
Elle est repérée ainsi : [cf. p.45] (u).

([i]N.B.
sur la version disponible sur internet, lire # là où il est écrit [x] :
le [x] provient d'une corruption de fichiers informatiques dus à des changements de format informatique; l'orginal porte bien un signe qui signifie dièse et non pas un x qui signifie double dièse. J'ai effectué la correction sur la copie ci-dessus. Le symbole dièse du manuscrit, au lieu d'être dessiné droit comme on fait maintenant, droit comme le signe + de l'addition, il est dessiné obliquement comme notre signe x de la multiplication (voyez le document pdf). D'où l'interprétation erronée effectuée par les logiciels de conversion de format.).
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

oui, mais... en pratique ?

Smile

sur http://www.scientillula.net/ , à rubrique physique, le logiciel HARMONIE

Pas aussi fin qu'on voudrait, mais permet d'approcher la chose en écoutant sons sans harmoniques dont la fréquence est voisine de la fréquence qu'on veut (par exemple, on peut écouter un son simple de fréquence 440 Hz, un autre de fréquence 261,6 Hz [mais pas 261 Hz], etc.)
_________________

Veit · Posté le: Sam Avr 15, 2006 6:49 pm Sujet du message: teentaal

Merci de tes compliments, Bahotatiah ! Very Happy

Mais le chapitre 8 que je suis en train d'écrire, c'est mon dada depuis des années et des années.

Par contre, ta réaction, elle porte sur le chapitre 6 dédié au rythme et qui, c'est vrai, mérite d'être développé (puisque la musique, c'est d'abord le rythme).
On avait déjà parlé de ça en février avec un garçon qui joue des tablas.

Idea

Ouvrons donc - et de suite ! - un sujet de discussion dédié au rythme - & bilingue de préférence.

Il commencera à cette adresse-ci : http://www.radioteentaal.com/forum/viewtopic.php?p=11415#11415

Veit · Posté le: Sam Avr 15, 2006 7:19 pm Sujet du message: 8 - 11 - a

8 - 11 - a spectre audio

Sur la pochette d'un microsillon 33 tours haute-fidélité des années soixante, le MD. 9006 des disques Vogue donnant l'enregistrement de trois opus pour orgue, de Bach, je lis :
le spectre sonore intégral --- tout ce que l'oreille humaine peut entendre --- :
de 30 cycles par seconde à 16000 cycles par seconde.

Autrement dit, le spectre audio s'étend de 30 Hz à 16 kHz
(1 kHz ça se dit " 1 kilo-hertz" et ça vaut 1000 Hz).
________________

Veit · Posté le: Lun Avr 17, 2006 1:27 am Sujet du message: 8 - 11 - b

8 - 11 - b théorème de Fourier

Le mathématicien Fourier a démontré que tout son musical peut s'analyser comme une somme de vibrations sinusoïdales de fréquences f, 2f, 3f, 4f, 5f, etc.

La vibration sinusoïdale est celle dont l'équation mathématique est la plus simple. C'est la plus facile à étudier.

La fréquence f est appelée fréquence fondamentale de la vibration.

Les termes de la somme, de fréquences 2f, 3f, 4f, 5f, etc., on les appelle les harmoniques du son fondamental.
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

8 - 10 - c timbre d'un instrument de musique

Le timbre d'une voix, d'un instrument de musique, c'est la suite des amplitudes des vibrations sonores de chacun des termes de la somme.

Le logiciel HARMONIE, dont on a a déjà parlé, offre la possibilité de composer artificiellement un timbre : c'est-à-dire à une vibration sinusoïdale de fréquence f et d'amplitude donnée (l'amplitude représente l'énergie), ajouter d'autres vibrations sinusoïdales de fréquences 2f, 3 f, etc.

Rester dans les multiples simples pour que le son soit musical.
Sinon, vous fabriquerez.... un bruit !

Le logiciel AUDACITY, autre logiciel téléchargeable gratuitement, fonctionne assez bien pour faire de l'analyse spectrale.

Mais si vous trouvez mieux pour donner la fréquence fondamentale, donnez-moi la référence, svp ! Car je me méfie des résultats d'Audacity et voudrais les étalonner.

(ici, à venir : autres logiciels d'analyse spectrale)

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

-
La fréquence 2 f c'est l'octave ;

- la fréquence 3 f, on verra que c'est celle de la douzième
(si on choisit l'échelle pythagoricienne
--- ou pratiquement celle de la douzième si on choisit l'échelle tempérée) ;

- la fréquence 4 f, c'est celle de la double octave ;

- la fréquence 5 f, on verra que c'est celle de la dix-septième
(si on choisit l'échelle harmonique
--- ou, à un comma près, celle de la dix-septième si on choisit l'échelle tempérée) ;

RAPPEL :
--- la 12ème, c'est.... Rolling Eyes

la quinte de l'octave
--- et la 17 ème, c'est.... Rolling Eyes

la tierce majeure de la double octave.
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Pour ces raisons qu'on reverra plus tard, on ne va pas chercher à produire des sons dont la fréquence fondamentale est en limite supérieure du spectre, mais en pratique on va rester 5 fois au-dessous. Au-delà, donc, de 16000 / 5 = 3200 Hz, on aura des sons très pauvres en harmoniques et pas jolis.

Qu'est-ce que ça peut bien être comme note que ces 3200 Hz ?
(1200/LN(2))*LN(3200/440) = 3435 points = 300 + (2*1200) + 735

En échelle chromatique tempérée :
On part du la3.de 440 Hz
On monte jusqu'au do4 (c'est les 300 points que l'on rajoute)
puis on va à do5, puis à do6 (c'est les + 2 * 1200 points),
puis on monte au sol6 en rajoutant 700 points.

Le sol#6, il est à 750 points, donc au-delà de la limite qu'on vient de définir.

Aisi, jusqu'au sol6, on aura des sons dont la qualité du point de vue de la richesse harmonique, sera bonne ou médiocre. Au-delà et dans la limite des fréquences audibles, les sons, on pourra les entendre mais il seront très pauvres en harmoniques, voire n'en auront pas.

Etant donnés la3 = 440 Hz et l'échelle chromatique tempérée, on a :
440 / 1,681 792 830 507 43 = 261,625 565 300 599 = do3

Retenons do3 = 261,6 Hz (tiens, cette valeur arrondie avec 1 seule décimale c'est justement celle que le logiciel HARMONIE nous permet d'entendre !), on a alors :

--> do3 = 261,6 Hz
--> do2 = 130,8 Hz
--> do1 = 65,4 Hz
--> do0 = 32,7 Hz

(1200/LN(2))*LN(32,7/30) = 149 points, proche de 150.

On pourrait donc aller chercher le son le plus grave (étant donnés un la de 440 Hz et une échelle chromatique tempérée, quelque part entre le si-1 ( qui est à 100 points sous le do0 ) et le sib-1 ( qui est à 200 points sous le do0 ).Seuls peut-être quelques rares grands orgues réalisent cela et produisent des sons de la gamme "-1".

Comme on est en train de la définir, l'étendue des sons qu'on va produire avec des instruments de musique ira du do0 au sol6.

Le la3 est-il au milieu de cette plage ?

Non, car de do0 à la3, on a :
-->____ 1200 points de do0 à do1
-->___+ 1200 points de do1 à do2
-->___+ 1200 points de do2 à do3
c'est-à-dire, déjà 3600 points
-->___+ 900 points de do3 à la3

Si on veut que le la3 soit au milieu, il faut donc, soit prendre comme note la plus basse celle qui est à 900 points au-dessus de do0, c'est-à-dire à la0 ; soit considérer comme note la plus haute la note qui est à 900 points au-dessus du sol6, c'est-à-dire un mi7.

je penche pour la 1ère hypothèse (l'étendue la plus restreinte des deux envsagées, pour l'orgue construit vers 1700) mais il nous faudrait consulter les documens relatifs aux orgues anciennes pour étayer cette assertion que j'ai rpétée, que le la a été choisi comme note de référence car c'est celle du milieu de l'étendue de l'orgue..

D'après théorie de la musique, par A. Danhauser, un livret de solfège publié à Paris aux éditions Henry Lemoine, au 17, rue Pigalle - j'en ai une réédition de 1929 -
(Pigalle est encore de nos jours un quartier de marchands d'instruments de musique) -, le piccolo monte jusqu'au la6.

Le que sais-je sur le son, le spectre sonore audible est plus étendu que ce qu'indique ma pochette de disque de... musique d'orgue (!) et on lit dans ce que sais-je (vers la page 45)

---> la note la plus grave utilisée en musique est :
do -1 = 16 Hz (environ)

---> la note la plus aiguë :
do 9 = 16700 Hz (ou à peu près)

Il est possible que l'échelle -1 existe sur l'orgue et que ma pochette de disque des années soixante ne soit pas une source fiable (la maison Vogue pourait en effet avoir indiqué non pas le spectre sonore audible, mais ce que que la technologie des années soixante permettait d'enregistrer et de reproduire !).

Par contre, je suis sceptique quant à la production de sons dans la 2ème moitié de l'échelle 7 et dans l'échelle 8 ; cependant, je ne peux a priori dire que l'auteur du que sais-je se trompe. Pour le savoir il faudrait le témoignage de quelqu'un connaissant bien les orgues ou éplucher de la documentation sur les grands orgues. Mais cela sort tout à fait du cadre du présent exposé.

Retenons donc, étendue des instruments de musique,
tous instruments confondus, et à l'exception du grand orgue : du do0 au la6.
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Vous lirez, sur l'un des documents internet en français dont je vous ai donné la référence, qu'il y a 3 octaves dans la musique indienne :
une moyenne, une aiguë au-dessus, une grave au-dessous. En fait, il y en a davantage.

Nous avons vu qu'en musique indienne on considère plutôt des septains que des octaves (un septain = un "saptak" ; une octave = une "ashtak").

Jacinthe, une amie de ma femme, m'a donné les noms des septains. Voici leur noms en tamoul (je retranscris phonétiquement) :

madhya sthayi = le septain médian

--- vers les graves, il y a :

mandra sthayi = le septain qui se tient en dessous

adhi-mandra sthayi = le septain qui se tient encore en dessous

--- vers les aigus, de l'autre côté du septan médian, il y a :

tar sthayi = le septain qui est dans l'aigu

N.B.
sthayi = saptaka
(le manuel en anglais écrit saptaka au lieu de saptak ; le a final est donc muet)

Considérer que l'étendue de la veena se trouve tout entière contenue dans 4 octaves correspond bien à la pratique.
Si on accordait la veena de Jacinthe de façon que SA = Do3, on aurait, pour note la plus grave, un Sol1, et pour note l plus aiguë, un Do5.

L'étendue de la guitare accordée de façon classique, c'est Mi1 / Si4.

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Reprenons la fréquence du sa proposée par Nameeta Shah et disons que ce sa, c'est un sa3. Nous avons alors :

sa3 = 240 Hz

d'où, en allant vers les graves :

sa2 = 120 Hz

sa1 = 60 Hz

sa0 = 30 Hz

De fait, Nameeta a donc choisi comme fréquence du SA une fréquence commode pour les calculs
mais aussi un point de départ de l'échelle, qui est la fréquence la plus grave du spectre sonore audible par l'oreille humaine.

En-dessous, c'est le domaine des infra-sons.

Dans l'aigu, au-delà de 16 à 20000 Hz, c'est le domaine des ultra-sons.
Pour garder une certaine richesse harmonique, on va en général se limiter à produire des sons musicaux d'une fréquence 5 fois moindre (20000 / 5 = 4000 ; 15000 / 5 = 3000).

Remontons à partir du sa3 :

sa3 = 240 Hz

sa4 = 480 Hz

sa5 = 960 Hz

sa6 = 1920 Hz

sa7 = 3840 Hz

3200 Hz = 1920 * (5/3) ==> c'est un Dha6

Donc, La limite supérieure des sons qu'on ira produire en musique indienne sera un Dha6, peut-être même un Ni6.

Dans tous les cas, on se tient à l'intérieur de 7 octaves, souvent moins.

On va voir maintenant l'étendue de quelques instruments, et le cas particulier des harpes (car les harpistes comptent les octaves autrement !)

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Voici l'étendue de quelques instruments (en sons réèls)

petite flûte (le piccolo de l'orchestre) : do4 / la6

petit "fifre" Yamaha YRF-21 (le mien) : do4 / mi 6
(et encore, il faut aller le chercher, ce mi !
du do 4 au ré 5 : c'est facile ;
ensuite, pour passer aux 2ème et 3ème modes de vibration de la colonne d'air : s'entraîner !)

flûte à bec soprano : do4 / ré 6

grande flûte traversière : do3 / do6

harmonica : do3 / do6

accordéon : do3 / mi5

violon : sol2 / do6

hautbois : si2 / mi5

trompette : sol2 / la4

clarinette : do#2 / fa5

guitare : mi 1 / sib4 (en accordage classique)

guitare : ré 1 / lab4 (en accordage DADGAD)

violoncelle : do1 / mi4

cor d'harmonie : si0 / fa4

contrebasse : mi0 / la2
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 352 Localisation: Tremblay (93)

Le clairseach

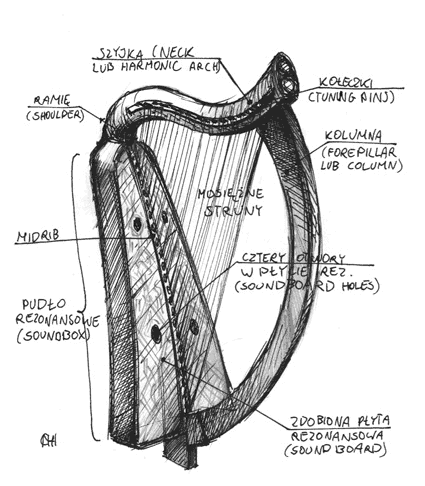
Le " clairseach " (prononcez Klèr-sèr ; c'est un mot gaélique) est une harpe écossaise à cordes métalliques
et dont la caisse de résonance est taillées dans la masse. C'est un instrument diatonique.

Parmi les artisans français facteurs de harpe : Violaine Alfaric,
qui est basée dans l'Aisne, réalise des clairseachs et des harpes celtiques.
Mme Alfaric a aussi réalisé un CD. http://www.alfaric.com/

La harpe celtique

Les harpes celtiques sont plus simples et comptent selon les modèles 34 cordes (comme le modèle illustré ci-dessus, l'Aida, de Salvi ; ici montée sur son petit tabouret)
ou 36 cordes mais quelquefois bien moins (23 ou 24). D'après un tarif de l'Instrumentarium (un des 2 magasins que je connaisse à Paris, l'autre étant la maison Budin),
une 36 cordes est une 34 cordes avec 2 cordes de plus vers le grave. Cependant, ce n'est pas là une règle absolue.

Cécile Corbel joue d'une harpe celtique de 34 cordes.
http://www.cecile-corbel.com/

Frédérique et Amanda, les harpistes de Deskomp, jouent de la harpe celtique à 36 cordes ( avez-vous déjà entendu le 3ème album de Deskomp ? Razz

Il y a dessus des morceaux joués à 3 harpes !) http://www.deskomp.org/

Un autre bon harpiste de la place de Paris est Hywel John, compère du guitariste gallois Jim Rowlands. http://jim.rowlands.free.fr/infos.htm

La palette utilisée sur la harpe celtique, qui est un levier associé à un ergot et qui permet de raccourcir la longueur de la corde vibrante, est une invention autrichienne (Tyrol ; vers 1700).

La grande harpe

= une Lyon & Healy, modèle "style 30" créé en 1958.

La grande harpe à 47 cordes, elle couvre l'étendue que nous avions déterminée la semaine dernière : du do 0 au sol 6.

Les grands fabricants de harpe sont :
- le Français CAMAC,
- l'Italien SALVI,
- l'Américain LYON & HEALY,
- le Japonais AOYAMA.
(Vous trouverez sans peine sur l'internet une liste mondiale de fabricants).

Il existe des grandes harpes à pédales à 40 cordes seulement.

La pédale -- qui va permettre à la harpe qui jusque là était un instrument diatonique, de devenir un instrument chromatique -- a été mise au point par Hochbruker en 1720. A cette époque, l'action sur la pédale hausse le son d'1/2 ton.

Les frères Cousineau perfectionnent le dispositif et en 1812, Sébastien Erard invente la pédale à double mouvement. Par exemple, si la corde à vide sonne ut bémol, une 1ère action sur la pédale (jusqu'à un cran) monte le son à ut, puis une 2ème action sur la pédale monte le son à ut dièse.

Les harpes chromatiques à nappes de cordes (2 rangs, voire 3 ;
[cherchez sur internet les harpes galloises triples (welsh triple harps)] ) sont apparues à cette époque (à ma connaissance : 1er inventeur = Gustave Lyon).

Les harpistes numérotent leurs cordes en partant de la plus aiguë. Ils comptent leurs octaves en allant de l'aigu vers le grave et les font aller de mi à fa en descendant.
Mais leur la3 est le même que le la3 général (ouf ! Smile

).
_________________