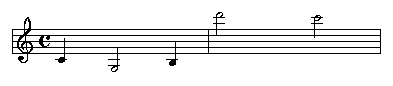|
***RaDio TEENTAAL***
100%
InDiAn MuSiC LiVe FrOm PaRiS
|
| retour
à la page zéro
|
| Auteur |
Message |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Mar Mai 09,
2006 11:56 pm Sujet
du message: 8 - 11- b - la portée de 11 lignes Posté le: Mar Mai 09,
2006 11:56 pm Sujet
du message: 8 - 11- b - la portée de 11 lignes |
|
|
Avant de faire un peu
d'arithmétique (si, si, si !  ), disons un
mot de la portée générale de 11 lignes... que vous n'avez
probablement jamais vu ! ), disons un
mot de la portée générale de 11 lignes... que vous n'avez
probablement jamais vu !
Tracez 5 lignes parallèles,
horizontales, équidistantes, comme ceci :
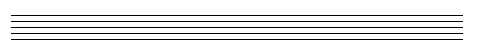
Tracez
1 ligne supplémentaire, au crayon noir si vous avez tracé les
autres au bic, au feutre ou à l'encre.
Votre ligne
supplémentaire, vous la placerez au-dessus ou au-dessous des 5
autres, comme vous voulez, mais de telle façon que vous ayez
maintenant 6 lignes équidistantes.
Complétez avec 5
autres lignes, comme celles formant la 1ère figure, et de façon à ce que la
ligne au crayon soit la ligne centrale de la figure finale.
Vous avez tracé la portée générale de 11 lignes.
Les 5 lignes du haut se numérotent de bas en haut,
comme ceci :

et les 5 lignes du bas, également.
Les 4
interlignes du haut se numérotent de bas en haut, comme ceci :

et les 4 interlignes du bas, également.
La portée générale de 11 lignes se compose :
-
d'une portée de 5 lignes, supérieure
- d'une portée de 5
lignes, inférieure
et d'une ligne centrale.
Les 11 lignes sont
équidistantes
Quand on écrit la musique sur 2
portées,
- on place une clef de sol pour marquer la place
d'un sol sur la portée du haut (généralement, il est sur la
2ème ligne),
- on place une clef de fa pour marquer la
place d'un fa sur la portée du bas(généralement, il est sur la
4ème ligne),
- on gomme la ligne centrale,
- et on
écarte les deux portées l'une de l'autre pour que l'ensemble
soit plus lisible,
- et puis on peut y ajouter, à gauche,
une accolade si les deux parties sont jouées par le même instrumentiste
Ca donne ceci :

[Sur ce dessin, le C,
c'est une indication de rythme à 4 temps]
La
ligne centrale, la ligne au crayon, la ligne qu'en général on
ne représente pas, c'est la ligne du middle C, la ligne du
milieu, la ligne du do3.
Pour rappeler
cette ligne gommée, on rajoute un petit trait, dit ligne
supplémentaire, de part et d'autre de la tête de la note qu'on
placerait sur cette ligne au crayon.
Voici un accord
où les notes sont, de bas en haut : do3, mi3, sol3, do4 .

Le la3, notre
note de référence, il est sur le 2ème interligne, ainsi :

Des lignes supplémentaires, on en rajoute
autant que nécessaire.
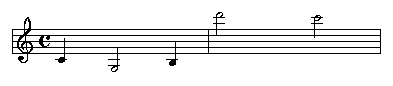
Les notes de cette mélodie sont, dans l'ordre où elles
apparaissent :
-- 1ère mesure : do3, sol2, si2 ;
-- 2ème mesure :
ré5, do5
Si on trace un
petit 8 au-dessus de la clef de sol, les notes sont jouées (ou
chantées) 1 octave au-dessus de ce qu'elles seraient en
l'absence de ce petit 8.
Si on trace un petit 8 au-dessous
de la clef de sol, les notes sont jouées (ou chantées) 1
octave au-dessous de ce qu'elles seraient en l'absence de ce
petit 8.
Et même chose en clef de fa.
Il existe
une clef d'ut [ ut =
do ] et on peut prendre, pour noter la musique, parmi les 11 lignes de la portée générale, 5 autres lignes que
les 5 du haut ou que les 5 du bas.
Il existe des instruments
transpositeurs qui ne jouent pas à la hauteur écrite, mais de
tout cela nous n'aurons pas besoin dans ce qui va suivre.
Source des figures =
http://www.arpegemusique.com/manuels.htm
_________________
Dernière édition par Veit le Mer Mai
10, 2006 12:48 am; édité 1
fois
| |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
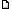 Posté le: Mer Mai 10,
2006 12:15 am Sujet
du message: 8 - 11 - c - Application pratique Posté le: Mer Mai 10,
2006 12:15 am Sujet
du message: 8 - 11 - c - Application pratique |
|
|

un la3 =
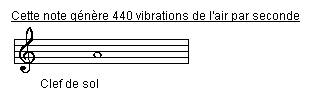
un
la3, puis un la2, puis un la1 =

Ce qui
à quoi on va s'intéresser maintenant, c'est :
- au do2 (en clé de fa 4ème ligne
: il est sur le 2ème interligne)
- au do3 (le do du milieu, sur la
ligne centrale entre les 2 portées)
- au sol3 (en clé de sol 2ème
ligne, sur la 2ème ligne)
Même si SA est choisi à
une hauteur qui est plus basse ou plus haute que le do3 du diapason de 440 Hz,
rien ne nous empêche de convenir d'une autre valeur du
diapason de façon à poser do3 = SA. Ce faisant, on réalise une
certaine transposition mais cela peut faciliter certains
raisonnements, certains réglages d'instruments aussi.
Je pense
que c'est cela qu'on appelle "s'accorder en
relatif".
_________________
Dernière édition par Veit le Mer Mai
10, 2006 12:48 am; édité 1
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Mer Mai 10,
2006 12:41 am Sujet
du message: 8 - 12 - a - retour à la tanpura Posté le: Mer Mai 10,
2006 12:41 am Sujet
du message: 8 - 12 - a - retour à la tanpura |
|
|
retour à la tanpura

Sur cette photo, on voit très bien
le chevalet plat
ainsi que les perles de réglage fin de la
tension des cordes
-- le même système se rencontre sur la
veena --

http://www.buckinghammusic.com/tanpura/tanpura.html
La tanpura, c'est l'instrument qui nous
rappelle sans cesse, tout ou long du raga,
- la note de base (notre
solfège l'appelle la tonique),
- ainsi que la note pivot
(notre solfège l'appelle la dominante)
- et puis la note
qui est à la basse de la note de base, 1 octave sous elle.
- PA = la dominante
- SA = la tonique (c'est la corde qui est en
double)
- *SA = la basse de la tonique
ATTENTION
!
À PARTIR DE MAINTENANT NOUS QUITTONS LE RÉGLAGE RÉGULIER DE
L'ÉCHELLE TEMPÉRÉE
ET NOUS PROCÉDONS À DES RÉGLAGES
DIFFÉRENTS.
NOUS ALLONS CONSTRUIRE UNE ÉCHELLE NON TEMPÉRÉE, DITE ÉCHELLE PYTHAGORICIENNE
(échelle de Pythagore).
Notation qu'on
va employer : f(SA) = fréquence du SA
On pose, par
définition, les fréquences relatives suivantes :
si f(*SA) = 1,
alors
f(SA) = 2
et
f(PA)
= 3
Autrement dit :
si
f(SA) = 1,
alors
f(*SA) = 1/2
et
f(PA) = 3/2
et
f(SA*) = 2
Et aussi :
si
f(do3) = 1,
alors
f(do2) = 1/2
et
f(sol3) = 3/2
et
f(do4) =
2
Partant de là, nous allons
construire méthodiquement notre échelle
et nous allons
trouver les shrutis que nous
avions placés dans un premier
groupe...
_________________
Dernière édition par Veit le Mer Mai
10, 2006 12:50 am; édité 1
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
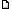 Posté le: Mer Mai 10,
2006 12:50 am Sujet
du message: 8 - 12 - b1 Posté le: Mer Mai 10,
2006 12:50 am Sujet
du message: 8 - 12 - b1 |
|
|
|
Continuons ces petits
calculs d'arithmétique en allant vers bas puis vers le haut de
l'échelle musicale.
 
dessin & photo de Mme Diane
Côté-Soleil, du Québec :
http://cafe.rapidus.net/diacote/lumiere/photos.html
Partons d'un do1
(Vous vous
rappelez ? C'est le do grave du violoncelle).
Ici,
dans le bas de la clef de fa :

Posons donc que la fréquence relative ce do1, par rapport à lui-même,
c'est... 1.
Notons cela :
do1 <----->
1
Alors nous
aurons :
do2 <----->
2
sol2 <----->
3
do3 <----->
4
sol3 <----->
6
do4 <----->
8
sol4 <----->
12
do5 <----->
16
sol5 <----->
24
do6 <----->
32
Là, on est
déjà bien haut, car pour monter au-dessus du
la5 avec le fifre en résine
YRF-21 de Yamaha, accroche-toi, Jeannot !

http://www.yamaha.co.jp/english/product/winds/product/recorder/f_s_sd_recorder/yrf_21/main.htm
P.S. A partir de
cette page-ci, il y a une navigation facile, instructive &


 sympa
sympa    à faire sur les principaux instruments de musique de
l'orchestre occidental : à faire sur les principaux instruments de musique de
l'orchestre occidental :
http://www.capcanal.com/couleurs/pages/episodes/03_violoncelle.htm
_________________
| |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
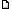 Posté le: Ven Mai 12,
2006 12:13 am Sujet
du message: 8 - 12- b2 Posté le: Ven Mai 12,
2006 12:13 am Sujet
du message: 8 - 12- b2 |
|
|
Faisons une représentation
graphique de cela.
Nous allons prendre comme échelle :
1 octave = 6 cm
Ainsi, si l'on place le
do1 dans le
bas d'une feuille A4 (21 cm x 29,7 cm), on pourra presque placer le
do6 en haut de
la feuille.
(On le pourrait si on tire le trait de
travers ou si on y colle une petite rallonge.
Le si5, lui, on
pourra le placer, c'est sûr !)
A cette échelle, 1 ton tempéré, c'est 1 cm
et 1/2 ton, c'est 1/2 cm (= 5 mm).
Il est
facile de placer tous les do : on va d'octave en
octave, donc de 6 cm en 6 cm, en partant du bas de l'échelle.
On sait repérer l'emplacement, sur cette grande règle,
des notes de l'échelle chromatique tempérée (les indiquer au
crayon noir léger !) car leurs emplacements sont des multiples
de 100 points (avec l'échelle choisie, 1 octave = 6 cm = 1200
points ; donc c'est facile).
 Mais le sol qui est à la quinte redoublée d'un do et
donc la fréquence vaut trois fois celle de ce do, comment le
placer ??? Mais le sol qui est à la quinte redoublée d'un do et
donc la fréquence vaut trois fois celle de ce do, comment le
placer ???
 Facile ! Facile !
On calcule la valeur de : 1200 * Log 3 / Log 2
et
on trouve : 1902 points
c'est-à-dire : 1200 + 702 points
On a aussi :
1200 * Log (3/2) / Log 2 = 1200 *
[Log 3 - Log 2] / Log 2 =
{1200 * [Log 3] / Log 2} - {
1200 * [Log 2] / Log 2 } = 1902 - 1200 = 702
Retenons
: 3/2 <-----> 702
points
Cet intervalle de
3/2 s'appelle la quinte
juste.
Vous avez sans doute
remarqué que les instruments indiens à cordes que nous avons
présentés s'accordent par quintes : on avait souvent des
cordes à vide qui sonnaient SA et PA.
Toujours en
supposant que l'on fixe notre diapason comme on veut, et en
supposant donc SA = do3, on voit qu'alors le
violoncelle serait accordé avec une note la plus grave qui
serait do1= **SA et
nous partirions de la note la plus grave du sarangi : do2= *SA.
 Vous pouvez reprendre ce qui a été exposé sur les étendues des
instruments à corde, voire même à vent, et les placer sur
cette échelle ;
Vous pouvez reprendre ce qui a été exposé sur les étendues des
instruments à corde, voire même à vent, et les placer sur
cette échelle ;
les placer aussi sur la portée et examiner les
rapports des fréquences entre
elles.
_________________
Dernière édition par Veit le Ven Mai
12, 2006 12:20 am; édité 2
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
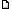 Posté le: Ven Mai 12,
2006 12:18 am Sujet
du message: 8 - 12 - c Posté le: Ven Mai 12,
2006 12:18 am Sujet
du message: 8 - 12 - c |
|
|
 Du PA au *SA,
il y a combien ? Du PA au *SA,
il y a combien ?
 Du sol3 au do4, il y a combien ? Du sol3 au do4, il y a combien ?
 4/3 4/3
On calcule :
4/3
<------> 498
points
Cet intervalle de
4/3 s'appelle la quarte juste
Remarque
: 498 + 702 =
1200
<==> Du *PA au SA, il y a une quarte
juste, puis une quinte juste du SA au PA
Du sol2 au do3, il y a une quarte
juste, puis une quinte juste du do3 au sol3
Et de même
ailleurs.
Par définition, on pose
MA = la note dont la
fréquence est 4/3
fois la fréquence du SA.
 La
fréquence du *MA est donc ?... La
fréquence du *MA est donc ?...
---  Je sais !!! Je sais !!!    La
fréquence du *MA est 2/3 !!! La
fréquence du *MA est 2/3 !!!
Rappelez-vous qu'une des
cordes du sitar, on l'accordait souvent PA et quelquefois MA,
selon le raga qu'on voulait jouer...
Eh bien, c'est
nécessairement en rapport avec ce que l'on vient d'exposer.
Vous pouvez maintenant placer tous les MA sur la
règle.
_________________
Dernière édition par Veit le Sam Mai
13, 2006 11:58 am; édité 1
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
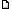 Posté le: Ven Mai 12,
2006 12:35 am Sujet
du message: 8 - 12 - d Posté le: Ven Mai 12,
2006 12:35 am Sujet
du message: 8 - 12 - d |
|
|
 Quelle est la
distance entre MA et PA ? Quelle est la
distance entre MA et PA ?
 expression en points expression en points
702
- 498 = 204
==> La distance entre MA et PA est 204
points.
 expression par une fraction expression par une fraction
( 3/2 ) / ( 4/3 ) = ( 3 * 3 ) / ( 2 * 4 ) = 9/8
==> La fréquence du PA est 9/8 fois la fréquence du
MA.
De même, la fréquence du sol3 est 9/8 fois la
fréquence du fa3.
Même chose pour sol1 par rapport à fa1, pour sol2 par rapport à fa2, pour sol4 par rapport à fa4, pour sol5 par rapport à fa5...
Autrement dit
:
==> la distance entre FA et SOL est 204 points ;
==> la fréquence du SOL est 9/8 fois la
fréquence du FA.
généralisation
Définition :
1 ton = 204
points
1 ton = 9 / 8
Le ton ainsi défini, nous lui donnons le nom de TON
MAJEUR PYTHAGORICIEN.
Ce ton,
nous l'appellons majeur ainsi parce qu'on rencontrera plus
tard la fraction 10/9
qui est un comma syntonique plus petite et que nous appellerons : 10/9 = TON MINEUR
PYTHAGORICIEN.
_________________
Dernière édition par Veit le Sam Mai
13, 2006 11:27 am; édité 1
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Sam Mai 13,
2006 2:34 am Sujet du
message: 8 - 12 - e1 Posté le: Sam Mai 13,
2006 2:34 am Sujet du
message: 8 - 12 - e1 |
|
|
Tétracordes
Un
tétracorde = un ensemble de 4 cordes fournissant 4 sons
musicaux.
Il en existe de plusieurs sortes, et c'est une
notion importante en solfège.
Nous avons dès à
présent de quoi construire 2 tétracordes semblables :
SA, RI, GA, MA
et
PA, DHA, NI, SA*
et, tout
pareillement
DO,
RE, MI, FA
et
SOL, LA, SI, do
Nous avons déjà
les notes DO, do, SOL, FA.
Il nous suffit de poser :
--- RE à 204 points au-dessus du DO
et
--- MI à
204 points au-dessus du RE
puis
--- LA à 204 points
au-dessus du SOL
et
---SI à 204 points au-dessus du LA
Fréquence du ré = [ 9/8 ] * fréquence du do
Fréquence du mi = [ 9/8 ] * fréquence du ré = [ 81/64 ] *
fréquence du do
Fréquence du la = [ 9/8 ] * fréquence
du sol = [ 27/16 ] * fréquence du do
Fréquence du si = [
9/8 ] * fréquence du la = [ 243/128 ] * fréquence du do
Ce qui donne pour le
si à l'octave inférieure une fréquence qui est celle du do de
référence, divisée par [ 256/243 ].
Et même chose en musique indienne.
On a déjà SA, *SA, PA et MA.
On définit ensuite
successivement, à partir de là :
RI et GA, et puis DHA et
NI.
Ce
faisant, c'est comme si nous montions le long des cordes SA et
PA de nos instruments à cordes : on a moyen ainsi de calculer
la position des frettes si l'instrument comporte des frettes,
et de calculer où placer les doigts, si on a un instrument
sans frettes.
_________________
Dernière édition par Veit le Dim Mai
14, 2006 8:42 pm; édité 2
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Sam Mai 13,
2006 3:49 am Sujet du
message: 8 - 12 - e2 Posté le: Sam Mai 13,
2006 3:49 am Sujet du
message: 8 - 12 - e2 |
|
|
Tétracordes (suite)
Ganesh nous avait groupé les shrutis par paquets.
Nous venons d'identifier certains des shrutis du 1er
paquet.
Je les écris en grands caractères dans le tableau
ci-dessous.
1er paquet :
(numérateurs et
dénominateurs ne sont que des puissances de 2 et de 3)
  Sa : 1 ( 0 ) Sa : 1 ( 0 )
 Re4 : 9/8 ( 204 ) Re4 : 9/8 ( 204 )
Ga1 : 32/27 ( 294 )
 Ga4 : 81/64 ( 408 ) Ga4 : 81/64 ( 408 )
  Ma1 : 4/3 ( 498 )
Ma1 : 4/3 ( 498 )
  Pa : 3/2 ( 702 )
Pa : 3/2 ( 702 )
Dha1 : 128 /81 ( 792 )
 Dha4 : 27/16 ( 906 ) Dha4 : 27/16 ( 906 )
Ni1 : 16/9 ( 996 )
Nous allons nous
intéresser aux propriétés des shrutis que nous avons trouvés,
puis aux autres shrutis de ce
paquet.
_________________
Dernière édition par Veit le Sam Mai
13, 2006 12:06 pm; édité 1
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Sam Mai 13,
2006 11:44 am Sujet
du message: 8 - 12 - e3 - 1 Posté le: Sam Mai 13,
2006 11:44 am Sujet
du message: 8 - 12 - e3 - 1 |
|
|
suite des quintes
A
connaître par coeur :
-- dans l'ordre des dièses, en
montant :
FA, DO, SOL, RE,
LA, MI, SI
-- dans l'ordre des bémols, en
descendant :
SI, MI, LA, RE,
SOL, DO, FA | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Dim Mai 14,
2006 1:44 am Sujet du
message: 8 - 12 - e3 - 2 Posté le: Dim Mai 14,
2006 1:44 am Sujet du
message: 8 - 12 - e3 - 2 |
|
|
Vu ce qu'on a posé plus
haut,
- monter d'une quinte, c'est multiplier une
fréquence par 3/2 ;
- descendre d'une quinte, c'est
diviser une fréquence par 3/2.
(N.B. : Diviser par 3/2,
c'est même chose que multiplier par 2/3).
Dans
l'espace image
(à savoir l'espace de notre feuille de papier et de ce que
nous y avons tracé
mais aussi l'espace de notre représentation mentale des choses,
représentation dans notre tête -- ce que fait l'ensemble
constitué par notre oreille et notre cerveau) :
- monter d'une
quinte, c'est monter de 702 points
- descendre d'une
quinte, c'est descendre de 702
points. | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Dim Mai 14,
2006 1:56 am Sujet du
message: 8 - 12 - e3 - 3 Posté le: Dim Mai 14,
2006 1:56 am Sujet du
message: 8 - 12 - e3 - 3 |
|
|
- Monter d'une quinte
redoublée c'est multiplier la fréquence par 3
-
Descendre d'une quinte redoublée c'est diviser la fréquence
par 3.
Prenons SA = 240 Hz = DO3.
C'est la
valeur qu'avait adoptée Nameeta Shah dans son mémoire de fin
d'étude de l'Université de Kanpur.
Elle a le grand
avantage de nous faciliter les calculs que nous allons faire.
Alors on a :
LA3 = (27 / 16) * 240 = 405
Hz
FA2 = (2/3)
* DO3 = 160 Hz
FA1 = (1/2) *
FA2 = 80 Hz
FA0 = (1/2) * FA1 = 40 Hz
Calculons les fréquences des notes en partant du FA0 et en montant.
Pour ce faire,
a) nous nous donnons la suite
des quintes (nous pouvons
l'observer sur l'échelle chromatique tempérée, qu nous donne
les noms des notes ; ici, nous reconstitutions une suite de
quintes non tempérées qui, historiquement, a précédé la
tempérée).
Fa, do,
sol, ré, la, mi, si,
la série continue ainsi :
Fa#, do#, sol#, ré#, la#,
mi#, si#,
puis la série continue encore ainsi :
Fa##, do##, sol##, ré##,
la##, mi##, si##
etc.
( N.B. En musique x est un symbole équivalent à
## )
Cela, c'est pour savoir quel nom donner aux notes
issues du calcul qu'on va décrire en b).
b) nous procédons à de simples
multiplications par 3.
et nous traçons nos
résultats sur le papier avec l'échelle : 1 octave = 6 cm.
On obtient :
FA0 = 40 Hz
3 *
FA0 = DO2 = 120 Hz
3 * DO2 =
SOL3 = 360 Hz
3 * SOL3 =
RE4 = 720 Hz
3 * RE4 =
LA6 = 2160 Hz
Au-delà de cet
aigu, on a des notes qui ne sont pas produites par nos
instruments de musique, mais qui existent cependant dans les
harmoniques de certaines de celles-ci.
Par contre,
leurs sous-multiples, eux, peuvent bel et bien être produits
par des instruments de musique convenablement conçus.
Remarque : de ces fréquences que nous venons de
trouver, nous tirons facilement les fréquences des FA, DO, SOL, RE, LA partout, en multipliant
ou en divisant convenablement par 2.
On remarquera
aussi que, avec la convention que l'on vient d'adopter, on a :
LA6 = 3 * RE4
RE4 = 3 * SOL3
SOL3 = 3 * DO2
DO2 = 3 * FA0
FA0 = 40 Hz
et donc
LA6
=
3 * RE4
=
9 * SOL3
=
27 * DO2
=
81 * FA0
Vous voyez pourquoi l'antique collaborateur de
l'empereur de Chine a eu l'idée de fractionner un gros, gros
bambou en 81 parties pour établir l'échelle musicale de
l'empire (pour en savoir
plus, lisez le 1er chapiter de Genesis of Music, de Harry
Partch).
Retenons : LA6 = (3^4)* FA0
 Hmmm, voyons un peu pour la mise en
page : de l'octave 0 à l'octave 6, ça nous fait 7 octaves. A
raison de 6 cm par octave, ça nous fait 42 cm. Hmmm, voyons un peu pour la mise en
page : de l'octave 0 à l'octave 6, ça nous fait 7 octaves. A
raison de 6 cm par octave, ça nous fait 42 cm.
Or, 42 = 2 *
21. Donc, avec une copie double (autrement dit une feuille au
format A3 : 42 x 29,7), on s'en tirera très bien
!
_________________
Dernière édition par Veit le Lun Mai
15, 2006 10:19 pm; édité 2
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Dim Mai 14,
2006 9:03 pm Sujet du
message: 8 - 12 - e3 - 4.1 Posté le: Dim Mai 14,
2006 9:03 pm Sujet du
message: 8 - 12 - e3 - 4.1 |
|
|
'Scusez, mais ça va être un
peu aride, maintenant.

 J'en vois qui souffrent ! Pire, ça va devenir de
plus en plus aride !... J'en vois qui souffrent ! Pire, ça va devenir de
plus en plus aride !... 

(= images prises
dans le désert de Thar)
On va
successivement s'intéresser à
- une suite de quintes ;
- une suite de quintes (ascendantes) et quartes
(descendantes) alternées.
_________________
Dernière édition par Veit le Lun Mai
15, 2006 10:33 pm; édité 1
fois | |
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Lun Mai 15,
2006 10:31 pm Sujet
du message: 8 - 12 - 4 - e3 - 4.2 Posté le: Lun Mai 15,
2006 10:31 pm Sujet
du message: 8 - 12 - 4 - e3 - 4.2 |
|
|

FA0 * 3/2 =
DO1
DO1 * 3/2 = SOL1
SOL1 * 3/2 = RE2
RE2 * 3/2 = LA2
LA2 * 3/2 = MI3
MI3 * 3/2 = SI3
SI3 * 3/2 = FA#4
FA#4 * 3/2 = DO#5
DO#5 * 3/2 = SOL#5
SOL#5 * 3/2 = RE#6
RE#6 * 3/2 = ( LA#6 ) Ce tableau
fournit évidemment des fréquences relatives des notes
considérées.
On y a simplifié l'écriture : " LA2 ", par exemple, y est
mis pour " fréquence du LA2 ".
J'y ai mis le
LA#6 entre
parenthèses, parce qu'il est plus haut que la note la plus
aiguë du piccolo
(revoir
le sous-chapitre consacré à l'étendue de la flûte, plus
haut).
  La photo du
chameau est tirée de http://www.wildlife-tour-india.com/ (parcs nationaux
de l'Inde et notices sur les grands animaux
sauvages). La photo du
chameau est tirée de http://www.wildlife-tour-india.com/ (parcs nationaux
de l'Inde et notices sur les grands animaux
sauvages).  
_________________
Dernière édition par Veit le Jeu Mai
18, 2006 12:53 am; édité 12
fois | |
| Revenir
en haut |
|
 |
Veit

Inscrit le: 25
Nov 2005
Messages: 325
Localisation: Tremblay
(93)
|
 Posté le: Lun Mai 15,
2006 10:47 pm Sujet
du message: 8 - 12 - 4 - e3 - 4.3² Posté le: Lun Mai 15,
2006 10:47 pm Sujet
du message: 8 - 12 - 4 - e3 - 4.3² |
|
|
Comme LA2 = (1/2) * LA3, il est possible
d'exprimer la fréquence de toutes ces notes en fonction de
LA3.
On peut
aussi trouver facilement moyen d'exprimer toutes les
fréquences en fonction de DO3
et aussi déduire des
fréquences identifiées celles de leurs notes homologues dans
les différentes octaves.
_________________
Dernière édition par Veit le Jeu Mai
18, 2006 12:44 am; édité 1
fois | |
 |
|