***RaDio TEENTAAL***

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Exprimées relativement au DO3, les fréquences relatives des homologues des notes identifiées jusqu'ici, et qui appartiennent à l'octave 3, sont, converties en points (i.e. en cents) :

DO3 = 1 <----> 0
RE3 = 9/8 <----> 204
MI3 = 81/64 <----> 408
FA3 = 4/3 <----> 498
SOL3 = 3/2 <----> 702
LA3 = 27/16 <----> 906
SI3 = 243 / 128 <----> 1110

DO#3 = 2187 / 2048 <----> DO3 + 114
RE#3 = 19683 / 16384 <----> RE3 + 114

FA#3 = 729 / 512 <----> FA3 + 114
SOL#3 = 6561 / 4096 <----> SOL3 + 114
LA#3 = 59049 / 32768 <----> LA3 + 114

_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Rappel : shrutis du 1er paquet

Sa : 1 ( 0 )

Re4 : 9/8 ( 204 )

Ga1 : 32/27 ( 294 )
Ga4 : 81/64 ( 408 )

Ma1 : 4/3 ( 498 )

Pa : 3/2 ( 702 )

Dha1 : 128 /81 ( 792 )
Dha4 : 27/16 ( 906 )

Ni1 : 16/9 ( 996 )

On ne trouve pas notre bonheur du côté des dièses Crying or Very sad

DONC, MÊME SI ON POSE SA = DO, MA TIVRA N'EST PAS L'EXACT EQUIVALENT D'UN FA# PYTHAGORICIEN

Cool

Cherchons donc du côté des bémols !
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Avant de passer aux bémols, on va revenir sur cette suite de quintes dans l'ordre des dièses (ou ordre ascendant)
pour la voir de façon plus simple et pour préparer ce qu'on va expliquer sur la suite de quintes dans l'ordre des bémols (ou ordre descendant).

Reprenons donc notre suite ascendante de quintes, mais en partant du DO du milieu. On forme ainsi :

(3/2)^0

<--------->

DO

(3/2)^1

<--------->

SOL

(3/2)^2

<--------->

ré

(3/2)^3

<--------->

la

(3/2)^4

<--------->

mi

(3/2)^5

<--------->

si

Et ceci en notant :

De là, on tire 6 notes de l'échelle diatonique
(il manque le FA qu'on calculera plus tard)

En poursuivant la suite, on a :
(3/2)^6 = 729/64 <---------> fa#6

De ce fa#6 = [3^6]/[2^6] = 729/64, on tire aisément :

fa#

Rrappel : cela en posant DO3 = 1.

En montant la suite des quintes, même si celle-ci n'a plus de réalité physique, on obtient des nombres dont on pourra déduire, par divisions successives par 2, d'autres nombres qui eux auront une réalité physique et qu'on appellera notes diésées, ou, le cas échéant, doublement diésées. (Ces notes, ce seront les notes de l'échelle diatonique, affectées d'un dièse ou d'un double dièse).

Ainsi, les fa# seront (modulo 2) des multiples ou des sous multiples de 3^6,
les do# des multiples ou des sous multiples de 3^7 (modulo 2), etc.
Comme ceci :

<--->

RESUME :
suite des quintes ascendantes : { (3/2)^n }, le point de départ de la suite étant un FA
L'ordre des termes de la suite des quintes ascendantes,
c'est l'ordre dans lequel on énonce les dièses qu'on place à la clef, dit : ordre des dièses
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Suite des quintes descendantes : { (2/3)^n }, le point de départ de la suite étant un SI
L'ordre des termes de la suite des quintes descendantes,
c'est l'ordre dans lequel on énonce les bémols qu'on place à la clef, dit : ordre des bémols

Considérons le si5. En fixant la référence (1) au do3, on a défini la fréquence du si5 relativement à cette référence, comme étant = (3/2)^5
Si on divise celle-ci par 3/2, on obtient celle du si4 = (3/2)^4

Et ainsi de suite, en effectuant des divisions successives par 3/2, on progresse par quintes en descendant.

En montant, on avait construit la suite de degrés que voici : "do sol, ré, la, mi, si".
En descendant, ces degrés, on les rencontre donc dans l'ordre suivant : si, mi, la , ré, sol, do.

La quinte en dessous du do3, c'est fa2.
Ce n'est pas sol2 : ce sol2 est à la quarte en-dessous du do3).

[ fa2 ] = [ do 3 ] / (3/2) = (2/3) * [ do 3 ]

( Diviser par 3/2, c'est même chose que multiplier par 2/3 ).

Poursuivant cette descente, nous posons, par définition :

[ sib1] = (2/3) * [ fa 2 ] = ( 4/9 ) * [ do3 ]

[ mib1] = (2/3) * [ sib1 ] = ( 8/27 ) * [ do3 ]

[ lab0] = (2/3) * [ mib1 ] = (16/81 ) * [ do3 ]

Si on pose do3 = 1
(c'est-à-dire fréquence du do3 = fréquence de référence pour nos calculs),
l'expression des fréquences se simplifie.

Idea On commence à voir des fractions qui ont un air de famille avec celles de nos shrutis du 1er paquet Smile
_________________
Dernière édition par Veit le Sam Mai 20, 2006 9:13 am; édité 4 fois

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Si on reprend le graphique que je vous avais invité à faire
(vous savez les 2 traits parallèles de 24 cm, gradués tous les 5 mm, celui de droite allant de do7 à DO3, celui de gauche allant de do4 à do0),
il est facile de représenter approximativement la suite descendante des quintes.

On part du si6, 1er harmonique du si3
(on construit le point marquant le si6 de façon à lire que la fréquence du si6 est le double de celle du si3)

702 points plus bas que le si6, on repère le mi6.

A l'échelle du graphique, on peut confondre 700 et 702 points.
On peut le faire pour se donner une idée de la chose.

Mais ces 2 points d'écart sont importants sur les plans théorique et historique,
car cumulés de quinte en quinte, ils vont faire qu'on aura un écart d'un comma sur la position de la note en bout de chaîne.

Pour la suite des quintes ascendantes, il en est de même, d'ailleurs, que pour la suite des quintes descendantes.

Au total, on construit aisément la suite :

(si6)
mi6
la5
ré5
sol4
do4
fa3
sib2
mib2
lab1
réb1
solb0
(dob-1)
(fab-1)

Comme on l'a dit, on passe d'un terme au suivant en divisant sa fréquence par 3/2, c'est-à-dire en multipliant sa fréquence par 2/3,
d'où que cette suite est résumée par la formule { (2/3)^n } .

On a aussi que l'expression de la fréquence de la famille des sons immédiatement tirés de cette suite sera, modulo 2, un multiple de 1/ (3^n).

Autrement dit, ce sont des fractions qui ont une puisance de 2 au numérateur et une puissance de 3 au dénominateur.

Muni de cette règle simple, nous allons maintenant examiner les shrutis de notre paquet n°1.
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

résumé, 1):

ordre des dièses : fa, do, sol, ré, la, mi, si

ordre des bémols : si, mi, la, ré, sol, do, fa

C'EST A SAVOIR PAR COEUR !
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

résumé, 2):

L'échelle musicale pythagoricienne (dite échelle de Pythagore), la plus antique du monde occidental, est basée sur les nombres 2 et 3.

Les fréquences des notes de cette échelle se construisent de la façon suivante et se déduisent toutes de la fréquence d'une seule note choisie comme fréquence de référence.

a) On forme la moitié d'une 1ère série en multipliant cette fréquence par 2 autant de fois que l'on veut ;
b) on forme l'autre moitié de la 1ère série en divisant cette fréquence par 2 autant de fois que l'on veut.

c) On forme la moitié d'une 2ème série en multipliant cette fréquence par 3 autant de fois que l'on veut ;
d) on forme l'autre moitié de la 2ème série en divisant cette fréquence par 3 autant de fois que l'on veut.

e) Au moyen de multiplications et de divisions successives par 2, on tire des ces séries 1 et 2 toutes les autres notes.

f) Notre connaissance de l'étendue des instruments de musique nous dit la signification des calculs que l'on effectue (la fréquence de référence ayant été choisie, on sait si les fréquences que l'on calcule ont une signification physique et si oui laquelle).

à Samos (l'île de Pythagore) au printemps http://www.samos.be/there/
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Pythagore puis après lui Aristoxène, Ptolémée et Zarlino ne raisonnaient pas sur des fréquences mais sur des longueurs de corde.

Rappelons que la longueur, c'est la grandeur inverse de la fréquence, la fréquence d'une corde vibrante étant inversement proportionnelle à la longueur de cette la corde -- c'est ce qui nous a servi à calculer l'emplacement des sillets sur le manche d'une guitare.

Vraisemblablement les Indiens de l'Antiquité aussi, puis leurs commentateurs ont aussi raisonné sur les longueurs de corde.
D'où peut-être que dans nos shrutis du 1er paquet, on rencontre des fractions de l'ordre des bémols et pas de fractions de l'ordre des dièses.

Aussi, on définira désormais le komal comme étant le bémol pythagoricien et on verra ultérieurement comment un tivra est proche des deux sortes de dièse que nous avons déjà définies, le tempéré du tempérament égal et le pythagoricien.

Les opérations arithmétiques (addition, soustraction, multiplication, division) étant des opérations commutatives
(on peut faire une suite d'opérations dans l'ordre qu'on veut, ça ne change pas le résultat - à condition de ne pas faire n'importe comment !),
on peut modifier, sans changer le résultat final, l'ordre des séquences a), b), c), d), e) du processus que l'on vient de décrire et en mixer les opérations.

Notamment, au lieu de faire des multiplications ou des divisions par 3, puis par 2, on peut d'emblée procéder à des multiplications et à des divisions par 3/2 : c'est ainsi qu'on construit la suite des quintes, puis on réalise les multiplications et divisions par 2 pour trouver les autres notes.

Diviser par 3/2 (= descendre d'une quinte), c'est multiplier par 2/3.
Multiplier encore par 2 revient à avoir multiplié par 4/3 (= monter d'une quarte).

De même, descendre d'une quinte, c'est descendre de 702 points.
Monter ensuite d'une octave, c'est monter de 1200 points.
On arrive ainsi à la note qui est 498 points au dessus de celle du départ, c'est-à-dire une quarte au-dessus d'elle, étant donné comme on a défini les quintes et les quartes justes.

La note de référence, on fixe sa fréquence comme on veut et on lui donne le nom qu'on veut (DO, LA, SA....) et on considère tout un univers de fréquences générées à partir d'elle grâce aux seuls nombres 2 et 3. Tel est l'univers musical pythagoricien.

Pour ce qui suit, nous appellerons DO et SA cette référence et nous lui associons le nombre 1.

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Le frère Mersenne a noirci des pages et des pages de calculs
(un exemplaire de son traité est disponible en libre consultation à la bibliothèque publique d'information (BPI) de Beaubourg,
à Paris, au-dessus du Centre Pompidou, au dernier étage en section musique).

Nous pourrions, comme lui, calculer toutes les fractions de l'échelle musicale en suivant la méthode décrite : multiplier 1 par 3/2 un certain nombre de fois ; puis d'une part multiplier successivement par 2 les résultats obtenus et d'autre part diviser successivement par 2 les résultats obtenus.

Grâce à Excel et à la formule d'Ellis, nous allons nous rendre compte rapidement de ce que cela donne en passant dans l'espace image.

Nous ferons cela en 4 temps.

1)
- Dans une feuille de calcul Excel, placer la valeur 0 dans la cellule M20 ;
- colorier la cellule M20 (en vert, par exemple) car elle sera notre cellule pivot ;
- dans la cellule A20, écrire do.

- Dans la cellule A19, écrire sol ;
- dans la cellule A18, écrire ré ;
- et ainsi de suite, monter la suite des quintes jusqu'en A1où il faudra avoir écrit si##.

- Dans la cellule A21, écrire fa ;
- dans la cellule A22, écrire sib ;
- et ainsi de suite, descendre la suite des quintes jusqu'en A35 où il faudra avoir écrit fabb.

- Ecrire que la cellule M19, c'est le contenu de la cellule qui est juste en-dessous (la M20) plus 702 points, c'est-à-dire, dans la cellule M19 taper la formule : = M20+702 ;
- recopier cette formule vers le haut, dans la colonne M, jusqu'à M1.

- Définir comme suit le contenu de la cellule M21 : =M20-702 ;
- recopier cette formule vers le bas, dans la colonne M, jusqu'à M35.

- Définir la cellule N20 comme étant la cellule M20, plus 1200 :
N20 = M20+1200
(Comme M20 = 0, on trouve comme résultat en N20 : 1200) ;
- recopier cette formule vers le haut et vers le bas dans la colonne N ;
- ainsi, de N1 à N35, on a une colonne N dont a défini chacune des cellules comme étant 1200 points au-dessus de sa cellule voisine qui est en colonne M.

- Recopier à droite toutes les formules de la colonne M, jusqu'en colonne V.

- De même, préparer un colonne L dont chacune des cellules est 1200 points en dessous de sa cellule voisine de la colonne M, puis recopier cela vers la gauche jusqu'en colonne B. Si l'on parcourt une ligne de M à B, on descend de 1200 points à chaque fois qu'on passe d'une colonne à la suivante. Le point de départ de cette programmation, c'est assigner à la cellule L20 la valeur : =M20-1200

On constitue ainsi une matrice de 21 x 35 = 735 valeurs définies chacune par une formule.

Dans l'espace réel, cela correspond à :
- multiplier successivement 1 (qui correspond au zéro placé en cellule M20) par 3/2 (en allant de M19 à M1) et à diviser successivement 1 par 3/2 (en allant de M21 à M35) ;
- en allant vers la droite, multiplier successivement par 2 le contenu des cellules ;
- en allant vers la gauche, diviser successivement par 2 le contenu des cellules.

2)
Copions maintenant (par un "copié / collage spécial") les valeurs de toutes les cellules renseignées, ainsi que la colonne A où nous avons mis le nom des notes, copions tout cela dans une deuxième feuille.

Examinons la diagonale et repérons (en les coloriant en jaune, par exemple) les cellules dont la valeur est comprise entre -1200 et +1200. On conserve la couleur verte à la cellule M20 qui contient la valeur 0.

Effaçons ensuite toutes les cellules non coloriées.
Puis copions le résultat dans une 3ème feuille.

3)
Dans la 3ème feuille, ligne par ligne, éliminons (supprimons) toutes les cellules vides comprises entre la colonne A (exclue) et la 1ère cellule colorée.

Ce faisant on réalise un tableau de 3 colonnes : une avec des noms de notes et les deux autres avec des chiffres.
En D20, il y a marqué 1200. La colonne D forme un 4ème colonne mais seule la cellule 20 de cette colonne contient une valeur.
4 valeurs de la colonne C sont vides (si##, ré##, sibb, mibb) mais pour ces notes, on a une indication en colonne B, donc ça va.

Copions dans une 4ème feuille ce qu'on vient de trouver.

4)
Dans la 4ème feuille, grâce à des copiés/collés judicieux, plaçons sur 2 colonnes A et B le nom des notes et leurs valeurs afin de trier cela.

On obtient une liste de 71 valeurs, que voici :

fab 1584
do 1200
rébb 1176
la## 1134
si 1110
dob 1086
la# 1020
sib 996
dobb 972
sol## 930
la 906
sibb 882
sol# 816
lab 792
fa## 726
sol 702
labb 678
mi## 636
fa# 612
solb 588
mi# 522
fa 498
solbb 474
ré## 432
mi 408
fab 384
ré# 318
mib 294
fabb 270
do## 228
ré 204
mibb 180
si## 138
do# 114
réb 90
si# 24
do 0
rébb -24
la## -66
si -90
dob -114
la# -180
sib -204
dobb -228
sol## -270
la -294
sol# -384
lab -408
fa## -474
sol -498
labb -522
mi## -564
fa# -588
solb -612
mi# -678
fa -702
solbb -726
mi -792
ré# -882
mib -906
fabb -930
do## -972
ré -996
do# -1086
réb -1110
si# -1176
do -1200
si##
ré##
sibb
mibb

Il faudrait, je crois, modifier un peu notre tableau 1 (l'étendre) pour avoir directement les 4 notes manquantes.
Je vous laisse le soin de les chercher par la méthode de votre choix mais on n'a pas besoin de ce résultat pour poursuivre notre exposé.
_________________
Dernière édition par Veit le Jeu Mai 25, 2006 9:37 am; édité 9 fois

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Reprenons la liste de nos shrutis du 1er paquet & cherchons les correspondances dans le tableau de valeurs ci-dessus,puis annotons cette liste. On trouve ceci :

Sa : 1 ( 0 ) <-----------> : DO

Re4 : 9 / 8 ( 204 ) <-----------> : RE

Ga1 : 32 / 27 ( 294 ) <-----------> : MIb
Ga4 : 81 / 64 ( 408 ) <-----------> : MI

Ma1 : 4 / 3 ( 498 ) <-----------> : FA

Pa : 3 / 2 ( 702 ) <-----------> : SOL

Dha1 : 128 / 81 ( 792 ) <-----------> : LAb
Dha4 : 27 / 16 ( 906 ) <-----------> : LA

Ni1 : 16/9 ( 996 ) <-----------> : SIb

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Le pavage de Cinthy

Voici un dessin que je dédie à Cinthy. C'est la synthèse de ce que nous avons vu jusqu'à présent.

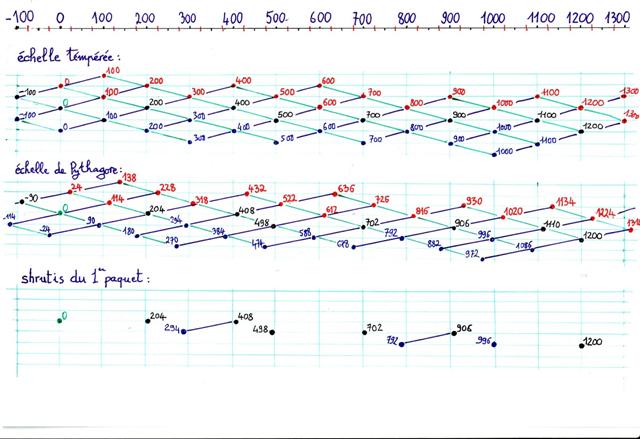
- Pavage tempéré (les carreaux sont des losanges)
Caractéristiques :
-- le ton vaut 200 points,
-- le 1/2 ton chromatique vaut 100 points,
-- le 1/2 ton diatonique vaut 100 points.

- Pavage pythagoricien ((les carreaux sont des parallélogrammes)
Caractéristiques :
- le ton vaut 204 points,
- le 1/2 ton chromatique vaut 114 points,
- le 1/2 ton diatonique vaut 90 points.

Pour ne pas surcharger le graphique, je n'ai pas prolongé la suite des quintes vers les triples dièses et triples bémols, mais on pourrait le faire.
Cependant cela n'aurait qu'un intérêt spéculatif et théorique, ces altérations compliquées n'étant pas usitées.

La même image en grand :
http://inventaire149.chez-alice.fr/imajindex/pythagore.jpg

_________________

cinthy · Modératrice Inscrit le: 20 Aoû 2005 Messages: 3021

Merci Veit, c'est très gentil de ta part de me dédier ce dessin.

Bonne continuation pour tes explications,

@+
Titi

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Dédicace expliquée + ... la suite du programme !

De rien, Cinthy Razz

!

A ce stade, on pourrait démarrer un laïus sur les modes, on pourrait parler du grégorien aussi. Pour le moment, retenons seulement qu'on a ce point d'embranchement possible ici. On y reviendra plus tard, si un jour on se met à discuter composition musicale ( Embarassed

je n'y connais rien, là !), arrangement des ragas.

Restant dans l'esprit du plan proposé par Ganesh, nous devrions retourner voir le manuel de d'Alembert et lire ce qu'il dit sur la génération de "l'échelle des Grecs", car cela nous une 1ère initiation aux bases de l'harmonie.

Nous ne passerons pas tout de suite à ce qu'il appelle "l'échelle des Modernes", par contre nous lirons les observations qu'il fit du violoncelle et nous en tirerons la notion d'harmoniques, ce qui nous permettra de comprendre les shrutis du 2ème paquet.

P.S.
Je ne n'ai pas oublié avoir promis un appendice sur l'échelle de Mercator-Holder,
c'est-à-dire l'échelle des violonistes qui divisent le ton en 9 parties, à savoir un demi-ton chromatique de 5 commas holdériens plus un demi-ton diatonique de 4 commas holdériens.
Mais ce sera pour la fin. On est sur une radio indienne, donc la compréhension des shrutis est prioritaire là-dessus.
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Oh ! Gosh ! I've got a problem !

Le problème qui se pose est un problème de constructeur de veena,
ou bien qui pourrait - j'imagine - être celui d'un régleur de sitar.
==> Faites part de votre expérience, svp !

Voici :
en regardant attentivement le motif du pavage de Cinthy, vous voyez que le motif partant du sa se répète à l'identique si l'on part du ma, mais que pour avoir un motif identique en partant du pa, il faudrait un ni pythagoricien mais...
... celui-ci n'est pas recensé parmi les shrutis du 1er paquet, et si l'on considère les shrutis du 2ème paquet, on voit qu'il n'y existe pas non plus !

Or, si l'on positionne les sillets de la veena, ou si l'on positionne les frettes du sitar de façon à jouer les shrutis du 1er paquet sur la corde sa,
on va forcément créer le shruti qui manque (ce ni) sur la corde pa,
alors pourquoi n'est - il pas recensé ?

La musique indienne ne retient que 22 shrutis. Y aurait - il parmi ceux-ci une valeur qui soit une approximation du shruti manquant ?
_________________

Veit · Inscrit le: 25 Nov 2005 Messages: 358 Localisation: Tremblay (93)

Il nous faut un Ni à 1110 points (243 / 128) et nous n'avons dans la liste que

Ni3 : 15/8 ( 1088 ) = un shruti tiré du 2ème paquet]
et
Ni4 : 31/16 ( 1145 ) = un shruti tiré du 3ème paquet]

Les écarts sont :
--> 1110 - 1088 = 22 points
et
---> 1145 - 1110 = 35 points

C'est donc le Ni3 qui est le plus proche du Ni pythagoricien. C'est lui qu'il faut considérer pour le moment.

Nous devons constater que ce Ni3 est 1 comma en dessous du Ni pythagoricien. Ce n'est pas négligeable car c'est avec des écarts d'1 comma (voire plus) par rapport à l'échelle pythagoricienne, qu'on va positionner les shrutis du 2ème paquet, tel que celui-là, dont on pourra dire qu'ils appartiennent à une échelle harmonique.

Je n'ai toujours pas pour l'instant d'explication au choix opéré par les musiciens indiens.
_________________